Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh. Giải chi tiết Giải bài 3 trang 122 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 3. Đường thẳng và mặt phẳng song song. Cho hình chóp S. ABCD có đáy ABCD là một hình bình hành….
Đề bài/câu hỏi:
Cho hình chóp S. ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm của tam giác SAB, I là trung điểm của AB và M là điểm thuộc cạnh AD sao cho \(AM = \frac{1}{3}AD\). Đường thẳng đi qua M và song song với AB cắt CI tại N. Chứng minh:
a) NG//(SCD);
b) MG//(SCD).
Hướng dẫn:
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
Lời giải:
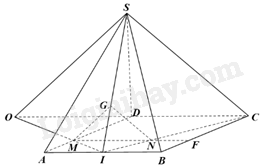
a) Gọi F là giao điểm của MN và BC.
Ta có: MN//AB, suy ra NF//BI (vì F thuộc MN, I thuộc AB)
Tam giác CIB có: NF//BI nên theo định lí Thalès ta có: \(\frac{{IN}}{{IC}} = \frac{{BF}}{{BC}}\) (1)
Mặt khác, \(AM = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)
Lại có MF///AB//DC nên \(\frac{{BF}}{{CB}} = \frac{{AM}}{{AD}} = \frac{1}{3}\) (2)
Từ (1) và (2) ta có: \(\frac{{NI}}{{CI}} = \frac{{BF}}{{BC}} = \frac{1}{3}\)
Vì G là trọng tâm của tam giác SAB nên \(\frac{{IG}}{{IS}} = \frac{1}{3}\)
Tam giác SIC có: \(\frac{{GI}}{{SI}} = \frac{{NI}}{{CI}} = \frac{1}{3}\) nên GN//SC (định lí Thalès đảo)
Vì GN//SC, \(SC \subset \left( {SDC} \right)\), GN không nằm trong mặt phẳng (SCD) nên NG//(SCD)
b) Trong mặt phẳng (ABCD), gọi O là giao điểm của MI và DC.
Trong tam giác OCI, có NM//OC suy ra \(\frac{{IM}}{{IO}} = \frac{{IN}}{{IC}} = \frac{1}{3}\) (định lí Thalès).
Tam giác SIO có: \(\frac{{IM}}{{IO}} = \frac{{IG}}{{IS}} = \frac{1}{3}\), suy ra MG//OS (định lí Thalès đảo)
Mà \(OS \subset \left( {SDC} \right)\), MG không nằm trong mặt phẳng (SCD). Do đó, MG//(SCD).