Đáp án Luyện tập 2 Bài 2. Phép tịnh tiến (trang 10, 11) – Chuyên đề học tập Toán 11 Kết nối tri thức. Hướng dẫn: Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O’; R) là ảnh của (O.
Câu hỏi/Đề bài:
Cho đường tròn (O; R) và điểm O’ khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O’, M không thẳng hàng, vẽ hình bình hành MOO’M’. Hỏi khi M thay đổi trên (O; R) thì M’ thay đổi trên đường nào?
Hướng dẫn:
Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O’; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \).
Lời giải:
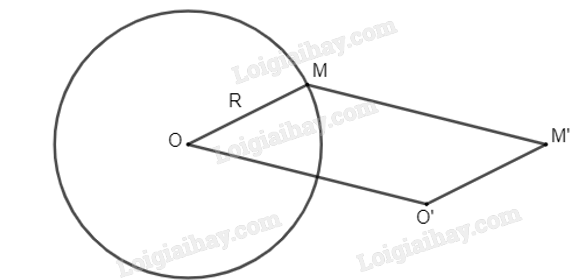
Ta có: MOO’M’ là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {O’M’} \) và \(\overrightarrow {OO’} = \overrightarrow {MM’} \)
Vì OM = R nên \(O’M’ = \left| {\overrightarrow {O’M’} } \right| = \left| {\overrightarrow {OM} } \right| = OM = R\) , R cố định nên O’ luôn cách M’ một khoảng không đổi bằng R.
Do O, O’ cố định và \(\overrightarrow {OO’} = \overrightarrow {MM’} \) nên phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \) biến điểm M thành điểm M’. Suy ra nếu M thay đổi trên (O; R) thì M’ luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \).
Lại có phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \) biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \) hay chính là điểm O’. Điều này có nghĩa là đường tròn (O’; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \).
Mà O’M’ = R không đổi nên M’ luôn thuộc đường tròn (O’; R).
Vậy khi M thay đổi trên (O; R) thì M’ thay đổi trên đường tròn (O’; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO’} \).