Giải Vận dụng 2 Bài 2. Phép tịnh tiến (trang 10, 11) – Chuyên đề học tập Toán 11 Kết nối tri thức. Gợi ý: Quan sát hình vẽ, dựa vào định nghĩa: Cho vectơ \(\overrightarrow u \).
Câu hỏi/Đề bài:
Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ \(\vec u\) có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?
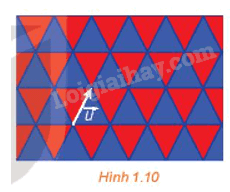
Hướng dẫn:
Quan sát hình vẽ, dựa vào định nghĩa: Cho vectơ \(\overrightarrow u \). Phép hiến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {MM’} = \overrightarrow u \) gọi là phép tịnh tiến theo \(\overrightarrow u \), kí hiệu \({T_{\overrightarrow u }}\). Vectơ \(\overrightarrow u \) được gọi là vectơ tịnh tiến.
Lời giải:
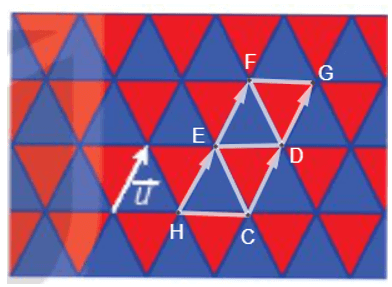
Đặt một số điểm như hình vẽ.
Ta thấy: \(\overrightarrow {HE} = \overrightarrow u ,\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm H, C, E tương ứng thành E, D, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác HCE thành tam giác EDF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu xanh thành một viên gạch màu xanh. Đối với các viên gạch màu xanh khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu xanh thành một viên gạch màu xanh. Ta cũng có: \(\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {DG} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm C, D, E tương ứng thành D, G, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác CDE thành tam giác DGF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu đỏ thành một viên gạch màu đỏ. Đối với các viên gạch màu đỏ khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu đỏ thành một viên gạch màu đỏ.