Lời giải Khám phá 2 Bài 2. Phép tịnh tiến (trang 12, 13) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Hướng dẫn: Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Câu hỏi/Đề bài:
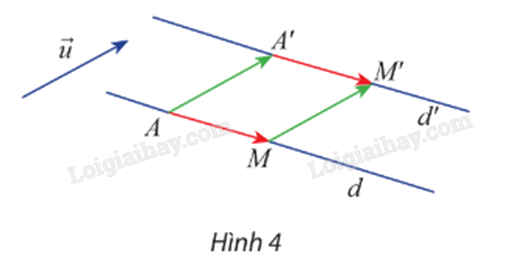
Cho vectơ \(\overrightarrow u \) và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến \({{\rm{T}}_{{\rm{\vec u}}}}\).
a) Hai vectơ ‘ có bằng nhau không?
b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.
Hướng dẫn:
Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải:
a) Ta có \({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{A}} \right) = {\rm{A’}}\), suy ra \(\overrightarrow {AA’} = {\rm{\vec u}}\).
\({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{M}} \right) = {\rm{M’}}\), suy ra \(\overrightarrow {MM’} = {\rm{\vec u}}\).
Khi đó \(\overrightarrow {AA’} = \overrightarrow {MM’} \,\,\,\left( { = {\rm{\vec u}}} \right)\).
Suy ra AA’ = MM’ và AA’ // MM’.
Vì vậy tứ giác AMM’A’ là hình bình hành.
Vậy \(\overrightarrow {{\rm{A’M’}}} = \overrightarrow {AM} \).
b) Gọi d’ là giá của \(\overrightarrow {{\rm{A’M’}}} \).
Vì A’M’ // AM (do tứ giác AMM’A’ là hình bình hành).
Nên d’ // d.
Vậy khi điểm M thay đổi trên d thì điểm M’ thay đổi trên d’ thỏa mãn \(\overrightarrow {MM’} = {\rm{\vec u}}\).