Lời giải Vận dụng 1 Bài 2. Phép tịnh tiến (trang 11) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Hướng dẫn: Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \.
Câu hỏi/Đề bài:
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Hướng dẫn:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM’} = \overrightarrow u \).
Nếu \(M'(x’;y’)\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x’ = x + a\\y’ = y + b\end{array} \right.\)
Lời giải:
Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {CC’} = \overrightarrow {DD’} = \overrightarrow {EE’} \).
Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\)
Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’.
Dựng \(\Delta AA’M\) vuông tại M (như hình vẽ).
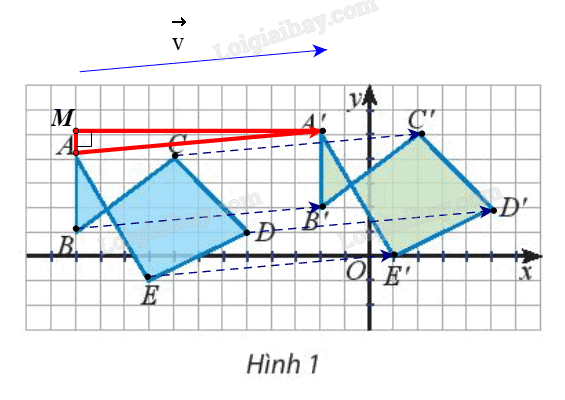
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A’M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị).
Suy ra \(AA’ = \sqrt {A{M^2} + {\rm{A’}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \).
Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA’} } \right| = AA’ = \sqrt {101} \)
Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).