Gọi \(D\) là điểm đối xứng với \(O\) qua \(B, \) \(F\) là điểm đối xứng với \(B\) qua \(D\) và \(G\. Phân tích, đưa ra lời giải Giải bài 4.14 trang 54 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 9. Tích của một vectơ với một số. Cho tam giác OAB vuông cân, với OA = OB = a….
Đề bài/câu hỏi:
Cho tam giác \(OAB\) vuông cân, với \(OA = OB = a.\) Hãy xác định độ dài của các vectơ sau \(\overrightarrow {OA} + \overrightarrow {OB} ,\,\,\overrightarrow {OA} – \overrightarrow {OB} ,\,\,\overrightarrow {OA} + 2\overrightarrow {OB} ,\,\,2\overrightarrow {OA} – 3\overrightarrow {OB} .\)
Hướng dẫn:
– Gọi \(D\) là điểm đối xứng với \(O\) qua \(B,\) \(F\) là điểm đối xứng với \(B\) qua \(D\) và \(G\) là điểm đối xứng với \(O\) qua \(A.\)
– Vẽ hình vuông \(OACB\) và hình chữ nhật \(OAED\)
Lời giải:
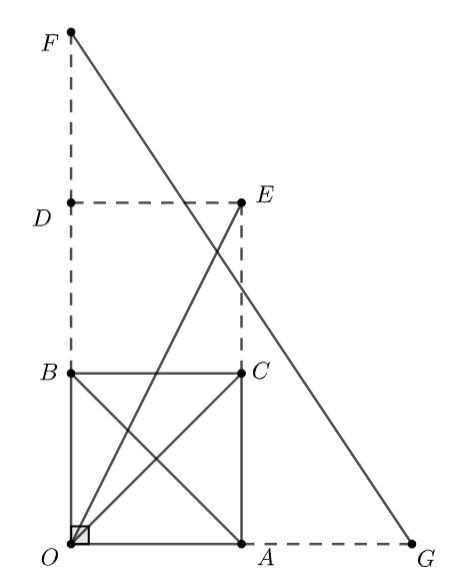
+) Theo quy tắc hình bình hành, \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \) với C là đỉnh thứ tư của hình bình hành \(OACB\)
Ta có: tứ giác \(OACB\) là hình bình hành
mặt khác \(\Delta OAB\) vuông cân tại \(A\)
nên tứ giác \(OACB\) là hình bình hành
\( \Rightarrow \) \(\left| {\overrightarrow {OC} } \right| = OC = \sqrt {O{A^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) Ta có: \(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} \)
Xét \(\Delta OAB\) vuông cân tại \(O\) có:
\( \Rightarrow \) \(\left| {\overrightarrow {AB} } \right| = AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) Gọi điểm \(D\) là điểm đối xứng với \(O\) qua \(B\)
\( \Rightarrow \) \(2\overrightarrow {OB} = \overrightarrow {OD} \) và \(OD = 2a.\)
Theo quy tắc hình bình hành, ta có: \(\overrightarrow {OA} + 2\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {OD} = \overrightarrow {OE} \) với \(E\) là điểm thứ tư của hình bình hành \(OAED\)
Ta có: tứ giác \(OAED\) là hình bình hành
Mặt khác \(\widehat {DOA} = {90^ \circ }\)
Nên tứ giác \(OAED\) là hình chữ nhật
Xét hình chữ nhật \(OAED\) có:
\( \Rightarrow \) \(\left| {\overrightarrow {OE} } \right| = OE = \sqrt {O{A^2} + O{D^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
+) Lấy điểm \(F\) đối xứng với \(B\) qua \(D\) và \(G\) đối xứng với \(O\) qua \(A\)
\( \Rightarrow \) \(2\overrightarrow {OA} = \overrightarrow {OG} ,\) \(3\overrightarrow {OB} = \overrightarrow {OF} ,\) \(OG = 2a,\)\(OF = 3a\)
Ta có: \(2\overrightarrow {OA} – 3\overrightarrow {OB} = \overrightarrow {OG} – \overrightarrow {OF} = \overrightarrow {FG} \)
Xét \(\Delta OFG\) vuông tại \(O\) có:
\( \Rightarrow \) \(\left| {\overrightarrow {FG} } \right| = FG = \sqrt {O{F^2} + O{G^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {2a} \right)}^2}} = a\sqrt {13} \)