Tính vectơ \(\overrightarrow {DE} \) Tính \(\overrightarrow {AB} \): \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DE} + \overrightarrow {EB} \) Tính \(\overrightarrow {BC} \). Hướng dẫn giải Giải bài 4.13 trang 54 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 9. Tích của một vectơ với một số. Cho tam giác ABC. Gọi D,E tương ứng là trung điểm của BC,CA….
Đề bài/câu hỏi:
Cho tam giác \(ABC.\) Gọi \(D,\,\,E\) tương ứng là trung điểm của \(BC,\,\,CA.\) Hãy biểu thị các vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {BC} ,\,\,\overrightarrow {CA} \) theo các vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BE} .\)
Hướng dẫn:
– Tính vectơ \(\overrightarrow {DE} \)
– Tính \(\overrightarrow {AB} \): \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DE} + \overrightarrow {EB} \)
– Tính \(\overrightarrow {BC} \): \(\overrightarrow {BC} = 2\overrightarrow {BD} = 2\left( {\overrightarrow {AD} – \overrightarrow {AB} } \right)\)
– Tính \(\overrightarrow {CA} \): \(\overrightarrow {CA} = \overrightarrow {DA} – \overrightarrow {DC} = – \overrightarrow {AD} – \overrightarrow {DC} \)
Lời giải:
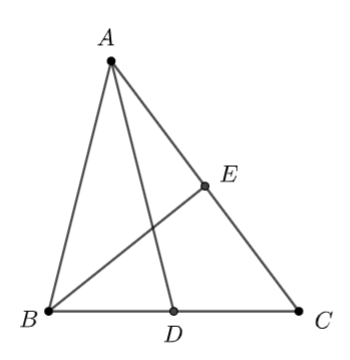
Ta có: \(DE\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(\overrightarrow {DE} = – \frac{1}{2}\overrightarrow {AB} \)
Ta có: \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DE} + \overrightarrow {EB} = \overrightarrow {AD} – \frac{1}{2}\overrightarrow {AB} + \overrightarrow {EB} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} = \overrightarrow {AD} – \overrightarrow {BE} \\ \Rightarrow \frac{3}{2}\overrightarrow {AB} = \overrightarrow {AD} – \overrightarrow {BE} \\ \Rightarrow \overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AD} – \overrightarrow {BE} } \right) = \frac{2}{3}\overrightarrow {AD} – \frac{2}{3}\overrightarrow {BE} \end{array}\)
Ta có: \(\overrightarrow {BC} = 2\overrightarrow {BD} = 2\left( {\overrightarrow {AD} – \overrightarrow {AB} } \right)\)
\(\begin{array}{l} = 2\left( {\overrightarrow {AD} – \frac{2}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BE} } \right)\\ = 2\left( {\frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BE} } \right) = \frac{2}{3}\overrightarrow {AD} + \frac{4}{3}\overrightarrow {BE} \end{array}\)
Ta có: \(\overrightarrow {CA} = \overrightarrow {DA} – \overrightarrow {DC} = – \overrightarrow {AD} – \overrightarrow {DC} \)
\(\begin{array}{l} = – \overrightarrow {AD} – \frac{1}{2}\left( {\frac{2}{3}\overrightarrow {AD} + \frac{4}{3}\overrightarrow {BE} } \right)\\ = – \overrightarrow {AD} – \frac{1}{3}\overrightarrow {AD} – \frac{2}{3}\overrightarrow {BE} \\ = – \frac{4}{3}\overrightarrow {AD} – \frac{2}{3}\overrightarrow {BE} \end{array}\)