Giải Hoạt động 4 Bài 1. Hàm số và đồ thị (trang 34, 35) – SGK Toán 10 Cánh diều. Hướng dẫn: Thay \({x_1} = – 1;{x_2} = 1\) vào tìm \({y_1} = f\left( {{x_1}} \right), {y_2} = f\left( {{x_2}} \right)\).
Câu hỏi/Đề bài:
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = – 1;{x_2} = 1\).
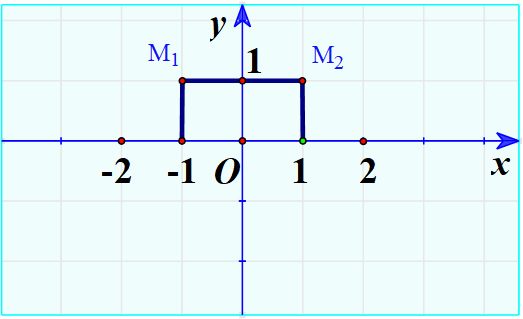
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
Hướng dẫn:
a) Thay \({x_1} = – 1;{x_2} = 1\) vào tìm \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\).
b) Xác định điểm và biểu diễn trên mặt phẳng.
Lời giải:
a) Thay \({x_1} = – 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:
\({y_1} = f\left( { – 1} \right) = {\left( { – 1} \right)^2} = 1\)
\({y_2} = f\left( 1 \right) = {1^2} = 1\)
b) Ta có \({x_1} = – 1;{y_1} = 1 \Rightarrow {M_1}\left( { – 1;1} \right)\)
Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)
Biểu diễn trên mặt phẳng: