Hướng dẫn giải Hoạt động 2 Bài 2. Hệ bất phương trình bậc nhất hai ẩn (trang 26, 27) – SGK Toán 10 Cánh diều. Gợi ý: Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.
Câu hỏi/Đề bài:
Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x – 2y \ge – 2\\7x – 4y \le 16\\2x + y \ge – 4\end{array} \right.\)
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình
trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
Hướng dẫn:
a) Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.
b) Miền nghiệm của hệ là miền nghiệm chung của 3 bất phương trình.
Lời giải:
a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x – 2y = – 2\);
\({d_2}:7x – 4y = 16\)
\({d_3}:2x + y = – 4\)
Thay tọa độ điểm O vào \(x – 2y\) ta được:
\(0 – 2.0 = 0 \ge – 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x – 4y\) ta được:
\(7.0 – 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge – 4\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
b)
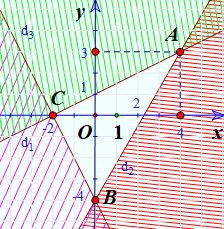
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.