Giải chi tiết Luyện tập – vận dụng 2 Bài 2. Hệ bất phương trình bậc nhất hai ẩn (trang 26, 27) – SGK Toán 10 Cánh diều. Gợi ý: Bước 1: Vẽ các đường thẳng.
Câu hỏi/Đề bài:
Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x – y > – 3\\ – 2x + 3y – 4\end{array} \right.\)
Hướng dẫn:
Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.
Lời giải:
Vẽ đường thẳng \(3x – y = – 3\) (nét đứt)
Thay tọa độ O vào \(3x – y > – 3\) ta được \(3.0 – 0 > – 3\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \( – 2x + 3y = 6\) (nét đứt)
Thay tọa độ O vào \( – 2x + 3y < 6\) ta được \( – 2.0 + 3.0 < 6\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \(2x + y = – 4\)(nét đứt)
Thay tọa độ O vào \(2x + y > – 4\) ta được \(2.0 + 0 > – 4\) (Đúng)
Gạch đi phần không chứa O
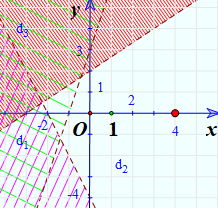
Miền nghiệm của hệ là phần không bị gạch chéo: