Quan sát đồ thị hàm số, trên \((a;b)\) + Đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên. Vận dụng kiến thức giải Giải bài 48 trang 62 SBT toán 10 – Cánh diều – Bài tập cuối Chương 3. Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 24…
Đề bài/câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 24
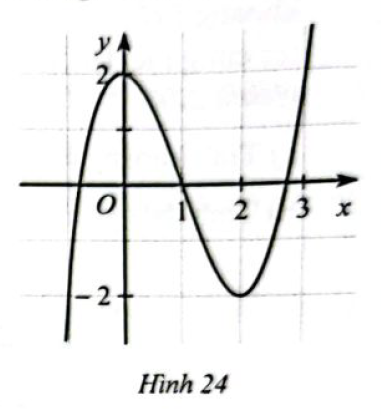
a) Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\)
b) Nêu tung độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục \(Oy\)
Hướng dẫn:
Quan sát đồ thị hàm số, trên \((a;b)\)
+ Đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên \((a;b)\)
+ Đồ thị hàm số đi xuống (từ trái qua phải) thì hàm số nghịch biến trên \((a;b)\)
Lời giải:
a) Quan sát đồ thị hàm số, ta thấy:
+ Đồ thị hàm số đi lên (từ trái qua phải) ứng với \(x \in \left( { – \infty ;0} \right) \cup (2; + \infty )\)
+ Đồ thị hàm số đi xuống (từ trái qua phải) ứng với \(x \in (0;2)\)
Do đó hàm số đồng biến trên các khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)và nghịch biến trên khoảng \(\left( {0;2} \right)\).
b) Giao điểm của hàm số với trục Oy có hoành độ là \(x = 0\)
Do đó tung độ của điểm đó là: \(y = f(0) = 2\)