Lời giải Hoạt động 3 Bài 2. Hypebol (trang 50, 51) – Chuyên đề học tập Toán 10 Cánh diều. Tham khảo: Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0, b > 0\).
Câu hỏi/Đề bài:
a) Quan sát điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) (Hình 15) và chứng tỏ rằng \(x \le – a\) hoặc \(x \ge a\)
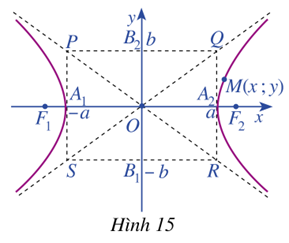
b) Viết phương trình hai đường thẳng PR và QS
Hướng dẫn:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Hình chữ nhật cơ sở có 4 đỉnh \(P\left( { – a;b} \right),Q\left( {a;b} \right),R\left( {a; – b} \right),S – \left( {a;b} \right).\)
+ Hai đường thẳng PR và QS lần lượt có phương trình \(y = – \frac{b}{a}x,y = \frac{b}{a}x\) được gọi là hai đường tiệm cận của hypebol (H)
Lời giải:
a) Nếu điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) thì \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\)
Vì \(\frac{{{y^2}}}{{{b^2}}} \ge 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} \ge \frac{{{y^2}}}{{{b^2}}} + 1 \Rightarrow {x^2} \ge {a^2} \ge \left[ \begin{array}{l}x \ge a\\x \le – a\end{array} \right.\)
b) Ta có: \(P\left( { – a;b} \right),R\left( {a; – b} \right) \Rightarrow \overrightarrow {PR} = \left( {2a; – 2b} \right)\)
Chọn \(\left( {b;a} \right)\) là 1 vector pháp tuyến của PR, khi đó phương trình đường thẳng PR là: \(PR:b\left( {x + a} \right) + a\left( {y – b} \right) = 0 \Leftrightarrow bx + ay = 0\) hay \(PR:y = – \frac{b}{a}x\)
Ta có: \(Q\left( {a;b} \right),S – \left( {a;b} \right) \Rightarrow \overrightarrow {QS} = \left( { – 2a; – 2b} \right)\)
Chọn \(\left( {b; – a} \right)\) là 1 vector pháp tuyến của QS, khi đó phương trình đường thẳng QS là: \(QS:b\left( {x – a} \right) – a\left( {y – b} \right) = 0 \Leftrightarrow bx – ay = 0\) hay \(QS:y = \frac{b}{a}x\)