Lời giải Hoạt động 1 Bài 2. Hypebol (trang 49) – Chuyên đề học tập Toán 10 Cánh diều. Hướng dẫn: Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0, b > 0\).
Câu hỏi/Đề bài:
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 13)
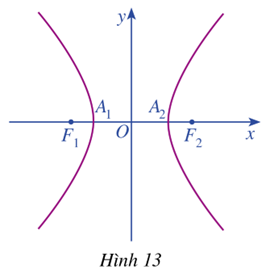
a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của hypebol \(\left( H \right)\)
b) Hypebol \(\left( H \right)\) cắt trục \(Ox\) tại các điểm \({A_1},{A_2}\). Tìm độ dài các đoạn thẳng \(O{A_1},O{A_2}\)
Hướng dẫn:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
Lời giải:
a) \({F_1},{F_2}\) là tiêu điểm của hypebol (H) có tọa độ \({F_1}( – c;0),{F_2}(c;0)\) với \(c = \sqrt {{a^2} + {b^2}} \)
b) \({A_1},{A_2}\) là giao điểm của (H) với Ox \( \Rightarrow {y_{{A_1}}} = {y_{{A_2}}} = 0 \Rightarrow \frac{{{x_{{A_1}}}^2}}{{{a^2}}} = 1;\frac{{{x_{{A_2}}}^2}}{{{a^2}}} = 1 \Rightarrow {x_{{A_1}}} = – a;{x_{{A_2}}} = a\)
Hay \({A_1}( – a;0),{A_2}(a;0)\) \( \Rightarrow O{A_1} = O{A_2} = a\)