Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) + Độ dài trục lớn: \(2a\), độ dài trục nhỏ: \(2b\. Lời giải Giải bài 5 trang 48 Chuyên đề học tập Toán 10 – Cánh diều – Bài 1. Elip – Chuyên đề học tập Toán 10 Cánh diều. Hình 11 minh họa mặt cắt đứng của một căn phòng trong bảo tàng với mái vòm trần nhà của…
Đề bài/câu hỏi:
Hình 11 minh họa mặt cắt đứng của một căn phòng trong bảo tàng với mái vòm trần nhà của căn phòng đó có dạng một nửa đường elip. Chiều rộng của văn phòng là 16 m, chiều cao của tường là 4 m, chiều cao của mái vòm là 3 m.
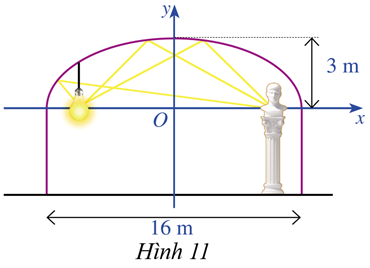
a) Viết phương trình chính tắc của elip biểu diễn mái vòm trần nhà trong hệ trục tọa độ \(Oxy\) (đơn vị trên hai trục là mét)
b) Một nguồn sáng được đặt tại tiêu điểm thứ nhất của elip. Cần đặt bức tượng ở vị trí có tọa độ nào để bức tượng sáng rõ nhất? Giả thiết rằng vòm trần phản xạ ánh sáng. Biết rằng, một tia sáng xuất phát từ một tiêu điểm của elip, sau khi phản xạ tại elip thì sẽ đi qua tiêu điểm còn lại
Hướng dẫn:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài trục lớn: \(2a\), độ dài trục nhỏ: \(2b\)
+ \(c = \sqrt {{a^2} – {b^2}} \)
Lời giải:
Gọi phương trình chính tắc của elip cần tìm là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Từ hình vẽ ta có:
Độ dài trục lớn: \(2a = 16 \Rightarrow a = 8\), độ dài bán trục nhỏ: \(b = 3\)
Vậy phương trình elip cần tìm là \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{9} = 1\)
b) Vì một tia sáng xuất phát từ một tiêu điểm của elip, sau khi phản xạ tại elip thi sẽ đi qua tiêu điểm còn lại nên để bức tượng sáng rõ nhất ta sẽ đặt bức tượng ở tiêu điểm còn lại. Toạ độ của vị trí này là \(\left( {c;0} \right)\)
Ta có: \(c = \sqrt {{a^2} – {b^2}} = \sqrt {{8^2} – {3^2}} = \sqrt {64 – 9} = \sqrt {55} \)
Cần đặt bức tượng cách tường bên phải một khoảng là: \(8 – \sqrt {55} \approx 0,58(m)\)