Trả lời Câu 4 trang 122 Vở thực hành Toán 9 – Bài tập cuối Chương 5. Gợi ý: Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó.
Câu hỏi/Đề bài:
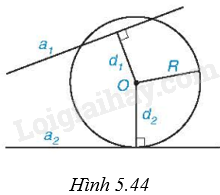
Cho đường tròn (O; R) và hai đường thẳng \({a_1}\) và \({a_2}\). Gọi \({d_1},{d_2}\) lần lượt là khoảng cách từ điểm O đến \({a_1}\) và \({a_2}\). Biết rằng (O) cắt \({a_1}\) và tiếp xúc với \({a_2}\) (H.5.44). Khi đó:
A. \({d_1} < R\) và \({d_2} = R\).
B. \({d_1} = R\) và \({d_2} < R\).
C. \({d_1} > R\) và \({d_2} = R\).
D. \({d_1} < R\) và \({d_2} < R\).
Hướng dẫn:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải:
Vì (O) cắt \({a_1}\) nên \({d_1} < R\). Vì (O) tiếp xúc với \({a_2}\) nên \({d_2} = R\).
Chọn A