Gọi \(R = \frac{{BC}}{2}\) là bán kính của đường tròn. + Nếu \(A \in \left( {O;R} \right)\) thì \(OA = R\). Khi đó. Phân tích, đưa ra lời giải Giải bài 5 trang 122, 123 vở thực hành Toán 9 – Bài tập cuối Chương 5. Cho đường tròn (O) đường kính BC và điểm A (khác B và C)….
Đề bài/câu hỏi:
Cho đường tròn (O) đường kính BC và điểm A (khác B và C).
a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì A nằm trên (O).
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
c) Với cùng giả thiết câu b, tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng \(BC = 6cm\).
Hướng dẫn:
a) Gọi \(R = \frac{{BC}}{2}\) là bán kính của đường tròn.
+ Nếu \(A \in \left( {O;R} \right)\) thì \(OA = R\). Khi đó, tam giác ABC có \(OB = OC = OA\) bằng R nên là trung tuyến ứng với cạnh huyền BC (góc BAC vuông).
+ Nếu tam giác ABC vuông tại A thì \(OA = OB = OC\) bằng R, nghĩa là \(AO = \frac{{BC}}{2} = R\). Do đó, điểm A nằm trên (O).
b) + Chứng minh tam giác ABO đều O vì \(OA = OB = AB = R\). Do đó, \(\widehat {ABO} = \widehat {ABC} = {60^o}\).
+ Tính được \(\widehat {BCA} = {30^o}\).
c) Tính góc AOC từ đó suy ra số đo cung AC nhỏ.
+ Độ dài cung AC là \(l = \frac{{120}}{{180}}.\pi .3\)
+ Diện tích của nó bằng \(S = \frac{{120}}{{360}}.\pi {.3^2}\)
Lời giải:
a) Gọi \(R = \frac{{BC}}{2}\) là bán kính của đường tròn.
Nếu \(A \in \left( {O;R} \right)\) thì \(OA = R\). Khi đó, tam giác ABC có \(OB = OC = OA\) bằng R nên là trung tuyến ứng với cạnh huyền BC (góc BAC vuông).
Ngược lại, nếu tam giác ABC vuông tại A thì trung tuyến OA bằng một nửa cạnh huyền BC, nghĩa là \(AO = \frac{{BC}}{2} = R\). Do đó, điểm A nằm trên (O).
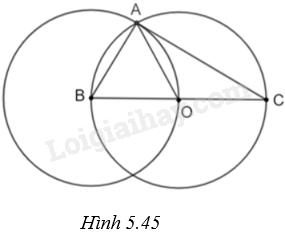
b) (H.5.45)
Vì \(BO = \frac{{BC}}{2} = R\) nên khi A là một trong hai giao điểm đường tròn (B; BO) với đường tròn (O) thì tam giác ABO đều O vì \(OA = OB = AB = R\). Do đó, \(\widehat {ABO} = \widehat {ABC} = {60^o}\).
Theo câu a, ABC là tam giác vuông tại A và có \(\widehat {ABC} = {60^o}\) nên \(\widehat {BCA} = {30^o}\).
c) Từ câu b, ta có \(\widehat {AOB} = {60^o}\), suy ra sđ$\overset\frown{AC}=\widehat{AOC}={{180}^{o}}-{{60}^{o}}={{120}^{o}}$.
Mặt khác \(R = \frac{{BC}}{2} = 3\left( {cm} \right)\) nên độ dài cung AC là \(l = \frac{{120}}{{180}}.\pi .3 = 2\pi \left( {cm} \right)\).
Hình quạt giới hạn bởi hai bán kính OA, OC ứng với cung \({120^o}\) nên diện tích của nó bằng \(S = \frac{{120}}{{360}}.\pi {.3^2} = 3\pi \left( {c{m^2}} \right)\).