Đáp án Câu 4 trang 101 Vở thực hành Toán 9 – Bài 14. Cung và dây của một đường tròn. Tham khảo: Trong một đường tròn, số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Câu hỏi/Đề bài:
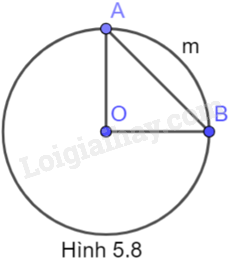
Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là
A. \({45^o}\).
B. \({90^o}\).
C. \({270^o}\).
D. \({60^o}\).
Hướng dẫn:
Trong một đường tròn, số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải:
Vì A, B thuộc (O) nên \(OA = OB = R\)
Ta có: \(A{B^2} = O{A^2} + O{B^2}\) nên tam giác OAB vuông tại O. Do đó, \(\widehat {AOB} = {90^o}\)
Vì góc ở tâm AOB chắn cung AmB nên \(sđ\overset\frown{AmB}=\widehat{AOB}={{90}^{o}}\)
Chọn B