Gọi H là giao điểm của đường vuông góc hạ từ M xuống AB, M’ là điểm đối xứng với M qua AB. Giải chi tiết Giải bài 1 trang 102 vở thực hành Toán 9 – Bài 14. Cung và dây của một đường tròn. Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó….
Đề bài/câu hỏi:
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}\).
Hướng dẫn:
+ Gọi H là giao điểm của đường vuông góc hạ từ M xuống AB, M’ là điểm đối xứng với M qua AB.
+ Chứng minh M’ thuộc đường tròn đường kính AB nên MM’ là một dây của đường tròn đường kính AB.
+ Do đó, \(MM’ \le AB\) hay \(2MH \le AB\), suy ra \(MH \le \frac{{AB}}{2}\).
Lời giải:
(H.5.9)
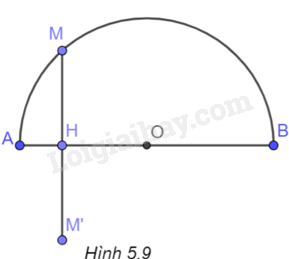
Gọi H là giao điểm của đường vuông góc hạ từ M xuống AB. Khi đó, độ dài đoạn MH là khoảng cách từ M đến AB. Gọi M’ là điểm đối xứng với M qua AB. Khi đó, H là trung điểm của MM’, tức là \(MM’ = 2MH\). Mặt khác do AB là đường kính của đường tròn nên M’ thuộc đường tròn đường kính AB. Suy ra MM’ là một dây của đường tròn. Do đó, \(MM’ \le AB\) hay \(2MH \le AB\), suy ra \(MH \le \frac{{AB}}{2}\).
Vậy khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}\).