Tam giác OHC vuông tại H có: \(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{{\frac{{\sqrt 3 }}{2}OA}}{{OA}} = \frac{{\sqrt 3 }}{2}\) nên tính được góc HOC. Phân tích và giải Giải bài 5 trang 103, 104 vở thực hành Toán 9 – Bài 14. Cung và dây của một đường tròn. Cho đường tròn (O; R). Gọi H là điểm thuộc bán kính OA sao cho (OH = frac{{sqrt 3 }}{2}OA)….
Đề bài/câu hỏi:
Cho đường tròn (O; R). Gọi H là điểm thuộc bán kính OA sao cho \(OH = \frac{{\sqrt 3 }}{2}OA\). Dây CD vuông góc với OA tại H. Tính số đo cung lớn CD.
Hướng dẫn:
+ Tam giác OHC vuông tại H có: \(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{{\frac{{\sqrt 3 }}{2}OA}}{{OA}} = \frac{{\sqrt 3 }}{2}\) nên tính được góc HOC.
+ Chứng minh OH là đường cao đồng thời là đường phân giác, từ đó tính được góc COD.
+ Số đo cung nhỏ CD bằng số đo góc COD, số đo cung lớn CD bằng 360 độ trừ đi số đo cung nhỏ CD.
Lời giải:
(H.5.13)
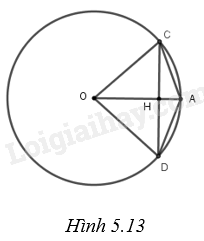
Xét đường tròn (O) có OH vuông góc với CD tại H nên H là trung điểm của CD. Xét tam giác OHC vuông tại H có:
\(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{{\frac{{\sqrt 3 }}{2}OA}}{{OA}} = \frac{{\sqrt 3 }}{2}\). Suy ra \(\widehat {HOC} = {30^o}\).
Mà tam giác OCD cân tại O \(\left( {OC = OD = R} \right)\) có OH là đường cao đồng thời là đường phân giác, suy ra \(\widehat {COD} = 2\widehat {COH} = {60^o}\)
Do đó, số đo cung nhỏ CD bằng \({60^o}\) và số đo cung lớn CD bằng \({360^o} – {60^o} = {300^o}\).