Góc nội tiếp ADC và góc ở tâm AOC cùng chắn cung nhỏ AC nên \(\widehat {ADC} = \frac{{\widehat {AOC}}}{2}\). Hướng dẫn trả lời Giải bài 4 trang 88 vở thực hành Toán 9 tập 2 – . Cho đường tròn (O) và hai dây cung AB,…
Đề bài/câu hỏi:
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) như hình bên.
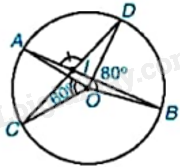
a) Biết rằng \(\widehat {AOC} = {60^o},\widehat {BOD} = {80^o}\). Tính số đo của góc AID.
b) Chứng minh rằng \(IA.IB = IC.ID\).
Hướng dẫn:
a) – Góc nội tiếp ADC và góc ở tâm AOC cùng chắn cung nhỏ AC nên \(\widehat {ADC} = \frac{{\widehat {AOC}}}{2}\).
– Góc nội tiếp BAD và góc ở tâm BOD cùng chắn cung nhỏ DB nên \(\widehat {BAD} = \frac{{\widehat {BOD}}}{2}\).
Do tổng ba góc trong tam giác AID bằng \({180^o}\) nên: \(\widehat {AID} = {180^o} – \widehat {IAD} – \widehat {IDA} = {180^o} – \widehat {ADC} – \widehat {BAD}\).
b) Chứng minh $\Delta IAC\backsim \Delta IDB\left( g.g \right)$, suy ra \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\), hay \(IA.IB = IC.ID\).
Lời giải:
a) Xét đường tròn (O), ta có:
– Góc nội tiếp ADC và góc ở tâm AOC cùng chắn cung AC nên \(\widehat {ADC} = \frac{{\widehat {AOC}}}{2} = {30^o}\).
– Góc nội tiếp BAD và góc ở tâm BOD cùng chắn cung DB nên \(\widehat {BAD} = \frac{{\widehat {BOD}}}{2} = {40^o}\).
Do tổng ba góc trong tam giác AID bằng \({180^o}\) nên:
\(\widehat {AID} = {180^o} – \widehat {IAD} – \widehat {IDA} = {180^o} – \widehat {ADC} – \widehat {BAD} = {110^o}\)
b) Hai tam giác IAC và tam giác IDB có: \(\widehat {AIC} = \widehat {DIB}\) (hai góc đối đỉnh), \(\widehat {CAI} = \widehat {CAB} = \widehat {CDB} = \widehat {IDB}\) (vì \(\widehat {CAB}\) và \(\widehat {CDB}\) là hai góc nội tiếp của (O) cùng chắn cung nhỏ $\overset\frown{CB}$)
Suy ra $\Delta IAC\backsim \Delta IDB\left( g.g \right)$. Do đó, \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\), hay \(IA.IB = IC.ID\).