Chứng minh \(\widehat {OAB} = \widehat {O’AC}\), \(\widehat {OBA} = \widehat {OAB}\), \(\widehat {O’AC} = \widehat {O’CA}\) nên \(\widehat {OBA} = \widehat {O’CA}\). Trả lời Giải bài 4 trang 118 vở thực hành Toán 9 – Bài 17. Vị trí tương đối của hai đường tròn. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A….
Đề bài/câu hỏi:
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng mỉnh rằng OB//O’C.
Hướng dẫn:
+ Chứng minh \(\widehat {OAB} = \widehat {O’AC}\), \(\widehat {OBA} = \widehat {OAB}\), \(\widehat {O’AC} = \widehat {O’CA}\) nên \(\widehat {OBA} = \widehat {O’CA}\).
+ Hai góc này ở vị trí so le trong nên OB//O’C.
Lời giải:
(H.5.37)
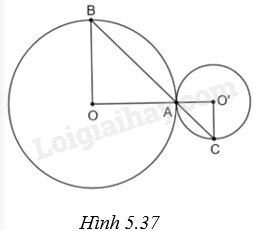
Do (O) và (O’) tiếp xúc ngoài với nhau tại A nên A thuộc OO’. Do đó, \(\widehat {OAB} = \widehat {O’AC}\) (hai góc đối đỉnh). Lại có \(\Delta OAB\) cân tại O \(\left( {OA = OB} \right)\) suy ra \(\widehat {OBA} = \widehat {OAB}\), \(\Delta O’AC\) cân tại O \(\left( {O’A = O’C} \right)\) suy ra \(\widehat {O’AC} = \widehat {O’CA}\). Từ đó suy ra \(\widehat {OBA} = \widehat {O’CA}\), mà hai góc này ở vị trí so le trong nên OB//O’C.