Bài 4 trang 114 vở thực hành Toán 9: Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm)

Đề bài/câu hỏi:

Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.

a) Chứng minh rằng chu vi của tam giác SEF=SA+SB.

b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng \(SE = SF\).

Hướng dẫn:

a) + Theo tính chất hai tiếp tuyến cắt nhau suy ra \(EA = ME\), \(FB = FM\).

+ Chu vi của \(\Delta \)SEF là:

\({P_{SEF}} = SE + EF + SF = SE + ME + MF + SF = \left( {SE + EA} \right) + \left( {FB + SF} \right) = SA + SB\).

b) + Theo tính chất hai tiếp tuyến cắt nhau suy ra \(SA = SB\) và SO là tia phân giác của góc ASB.

+ Chứng minh SAB cân tại S nên SO là đường phân giác nên đồng thời là đường cao suy ra \(SO \bot AB\).

+ Chứng minh EF//AB.

+ Chứng minh \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\), mà \(SA = SB\), do đó \(SE = SF\)

Lời giải:

(H.5.31)

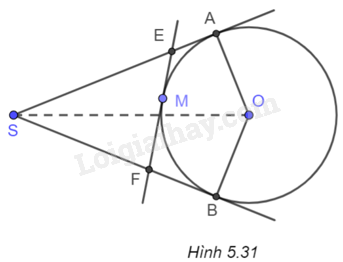
a) Xét hai tiếp tuyến của (O) cắt nhau tại E ta có \(EA = ME\). Tương tự, có \(FB = FM\).

Chu vi của tam giác SEF là

\({P_{SEF}} = SE + EF + SF = SE + ME + MF + SF = SE + EA + FB + SF\)

\( = \left( {SE + EA} \right) + \left( {FB + SF} \right) = SA + SB\) (điều phải chứng minh)

b) Giả sử M trùng với giao điểm của SO và (O).

Xét hai tiếp tuyến SA, SB của (O) cắt nhau tại S, ta có \(SA = SB\) và SO là tia phân giác của góc ASB.

Tam giác SAB cân tại S (do \(SA = SB\)) có SO là đường phân giác nên đồng thời là đường cao của tam giác, tức là \(SO \bot AB\).

EF là tiếp tuyến của (O) tại M nên \(EF \bot SO\).

Từ đó suy ra EF//AB (cùng vuông góc với SO).

Tam giác SAB có EF//AB nên \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\), mà \(SA = SB\), do đó \(SE = SF\) (điều phải chứng minh)