Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O. Vận dụng kiến thức giải Giải bài 4 trang 108 vở thực hành Toán 9 tập 2 – . Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo…
Đề bài/câu hỏi:
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều \({45^o}\) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
Hướng dẫn:
a) Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) + Chứng minh các tam giác AOE, BOF, COG, DOH, EOD, FOA, GOB, HOC bằng nhau theo trường hợp cạnh-góc-cạnh.
Suy ra EA = AF = FB = BG = GC = CH = HD = DE.
+ Bát giác \(EAFBGCHD\) lồi có các cạnh bằng nhau và nội tiếp đường tròn \((O).\)
Suy ra, các đỉnh của bát giác chia đường tròn thành 8 cung nhỏ với số đo mỗi cũng là 45o.
Từ đó, tính được các góc của bát giác bằng nhau và bằng 270 độ.
Do đó, \(EAFBGCHD\) là bát giác đều.
Lời giải:
a) Các điểm \(E,F,G,H\) cùng nằm trên đường tròn \(\left( O \right)\) và được vẽ như hình bên.
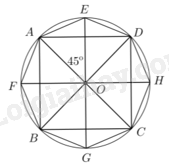
Do \(\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = {45^ \circ }\) nên \(\widehat {EOD} = \widehat {FOA} = \widehat {GOB} = \widehat {HOC} = {45^ \circ }\) (vì các tam giác\(AOD,BOA,COB,DOC\) vuông cân tại O).
Do vậy các tam giác AOE, BOF, COG, DOH, EOD, FOA, GOB, HOC bằng nhau theo trường hợp cạnh-góc-cạnh.
Suy ra EA = AF = FB = BG = GC = CH = HD = DE.
Vậy bát giác \(EAFBGCHD\) lồi có các cạnh bằng nhau và nội tiếp đường tròn \((O).\)
Hơn nữa các đỉnh của bát giác chia đường tròn thành 8 cung nhỏ với số đo mỗi cũng là 45o.
Do vậy các góc của bát giác lồi là các góc nội tiếp chắn đúng 6 cung nhỏ trên nên bằng nhau và có số đo bằng \(\frac{6}{8}{.360^ \circ } = {270^ \circ }\).
Vậy \(EAFBGCHD\) là bát giác đều.