Theo hình vẽ, ta thấy\(MBNPDQ\) là lục giác lồi. + Gọi \(a\. Gợi ý giải Giải bài 4 trang 104 vở thực hành Toán 9 tập 2 – . Cho hình thoi ABCD có (widehat A = {60^o}). Gọi M, N, P,…
Đề bài/câu hỏi:
Cho hình thoi ABCD có \(\widehat A = {60^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Hướng dẫn:
+ Theo hình vẽ, ta thấy\(MBNPDQ\) là lục giác lồi.
+ Gọi \(a\) là độ dài cạnh hình thoi thì \(BM = BN = DP = DQ = \frac{a}{2}.\)
+ Chứng minh tam giác AMQ và CNP là các tam giác đều nên \(MQ = AM,\,\,NP = CP\), \(\widehat {QMB} = {180^{\rm{o}}} – \widehat {QMA} = {120^{\rm{o}}}.\)
+ Chứng minh tương tự \(\widehat {BNP} = \widehat {NPD} = \widehat {DQM} = {120^{\rm{o}}}.\)
+ Vì \(ABCD\) là hình thoi nên \(\widehat {MBN} = \widehat {PDQ} = {180^{\rm{o}}} – \widehat A\).
+ \(MBNPDQ\) là lục giác lồi có tất cả các cạnh và các góc bằng nhau và do đó là lục giác đều.
Lời giải:
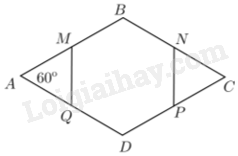
Theo hình vẽ, ta thấy\(MBNPDQ\) là lục giác lồi. Gọi \(a\) là độ dài cạnh hình thoi. Như vậy: \(BM = BN = DP = DQ = \frac{a}{2}.\)
Mặt khác, các tam giác cân \(AMQ\) và \(CNP\) có \(\widehat A = \widehat C = {60^{\rm{o}}}\) nên chúng là tam giác đều.
Do đó \(MQ = AM = \frac{a}{2},\,\,NP = CP = \frac{a}{2}.\) Hơn nữa \(\widehat {QMB} = {180^{\rm{o}}} – \widehat {QMA} = {120^{\rm{o}}}.\)
Tương tự, \(\widehat {BNP} = \widehat {NPD} = \widehat {DQM} = {120^{\rm{o}}}.\)
Vì \(ABCD\) là hình thoi nên \(\widehat {MBN} = \widehat {PDQ} = {180^{\rm{o}}} – \widehat A = {120^{\rm{o}}}.\) Vậy \(MBNPDQ\) là lục giác lồi có tất cả các cạnh và các góc bằng nhau và do đó là lục giác đều.