Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\). Giải và trình bày phương pháp giải Giải bài 3 trang 95 vở thực hành Toán 9 tập 2 – . Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như hình bên….
Đề bài/câu hỏi:
Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như hình bên.
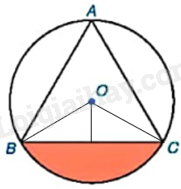
a) Tính bán kính R của đường tròn (O).
b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.
Hướng dẫn:
a) Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
b) + Tính S’ là diện tích hình quạt chắn cung nhỏ BC, tính diện tích tam giác BOC.
+ Khi đó, \(S = S’ – {S_{BOC}}\).
Lời giải:
a) Ta có: \(R = \frac{{\sqrt 3 }}{3}BC = \sqrt 3 \left( {cm} \right)\).
b) Bán kính đường tròn nội tiếp tam giác ABC là: \(r = \frac{{\sqrt 3 }}{6}BC = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\).
Chiều cao từ đỉnh O xuống cạnh BC của \(\Delta BOC\) bằng bán kính đường tròn nội tiếp tam giác ABC. Do vậy, \({S_{BOC}} = \frac{1}{2}r.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\).
Ta có: \(\widehat {BOC} = 2.\widehat {BAC} = {120^o}\). Diện tích hình quạt chắn cung nhỏ BC là: \(S’ = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)\).
Diện tích hình viên phân cần tính là: \(S = S’ – {S_{BOC}} = \pi – \frac{{3\sqrt 3 }}{4} \approx 1,84\left( {c{m^2}} \right)\).