Bán kính đường tròn đáy của hình nón là: \(R = \left( {35 – 2. 10} \right): 2 = 7, 5\left( {cm} \right)\). Phân tích và giải Giải bài 3 trang 122, 123 vở thực hành Toán 9 tập 2 – . Chiếc mũ của chú hề với các kích thước như hình bên….
Đề bài/câu hỏi:
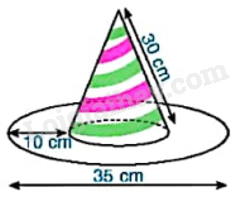
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của \(c{m^2}\)).
Hướng dẫn:
+ Bán kính đường tròn đáy của hình nón là: \(R = \left( {35 – 2.10} \right):2 = 7,5\left( {cm} \right)\).
+ Tính diện tích xung quanh hình nón có bán kính \(35:2\left( {cm} \right)\) và đường sinh 30cm.
+ Diện tích vành mũ bằng hiệu diện tích hình tròn bán kính \(35:2cm\) và diện tích hình tròn bán kính \(\)\(\left( {35:2 – 10} \right)cm\).
+ Diện tích vải cần dùng bằng tổng diện tích xung quanh của hình nón và diện tích vành mũ.
Lời giải:
Bán kính đường tròn đáy của hình nón là \(\left( {35 – 2.10} \right):2 = 7,5\left( {cm} \right)\).
Diện tích xung quanh của hình nón là:
\({S_1} = \pi Rl = \pi .7,5.30 = 225\pi \left( {c{m^2}} \right)\).
Diện tích vành mũ (hình vành khăn) là:
\({S_2} = \pi .{\left( {35:2} \right)^2} – \pi .{\left( {15:2} \right)^2} = 250\pi \left( {c{m^2}} \right).\)
Diện tích vải cần để làm chiếc mũ là:
\(S = {S_1} + {S_2} = 225\pi + 250\pi = 475\pi \approx 1492,3\left( {c{m^2}} \right).\)