Tính thể tích \({V_1}\) của hình trụ có bán kính \(AH = 3cm\), chiều cao \(AB = 12cm\). + Tính thể tích \({V_2}\. Phân tích, đưa ra lời giải Giải bài 10 trang 128 vở thực hành Toán 9 tập 2 – . Tính thể tích hình tạo thành khi cho hình bên quay quanh IH một vòng….
Đề bài/câu hỏi:
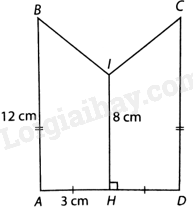
Tính thể tích hình tạo thành khi cho hình bên quay quanh IH một vòng.
Hướng dẫn:
+ Tính thể tích \({V_1}\) của hình trụ có bán kính \(AH = 3cm\), chiều cao \(AB = 12cm\).
+ Tính thể tích \({V_2}\) của hình nón có đường kính \(BC = 6cm\), chiều cao \(h = 12 – 8 = 4\left( {cm} \right)\).
+ Thể tích hình được tạo thành: \(V = {V_1} – {V_2}\)
Lời giải:
Thể tích hình trụ có bán kính \(AH = 3cm\), chiều cao \(AB = 12cm\) là:
\({V_1} = \pi {.3^2}.12 = 108\pi \left( {c{m^3}} \right)\).
Thể tích hình nón có đường kính đáy \(BC = 6cm\), chiều cao \(h = 12 – 8 = 4cm\) là:
\({V_2} = \frac{1}{3}\pi {.3^2}.4 = 12\pi \left( {c{m^3}} \right)\).
Thể tích của hình tạo thành là:
\(V = {V_1} – {V_2} = 108\pi – 12\pi = 96\pi \left( {c{m^3}} \right)\).