Gọi M là trung điểm của BC. + Chứng minh \(ME = MB = MC = MF\). Suy ra đường tròn \(\left( {M, MB} \right)\. Gợi ý giải Giải bài 1 trang 106 vở thực hành Toán 9 tập 2 – . Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD,…
Đề bài/câu hỏi:
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Hướng dẫn:
+ Gọi M là trung điểm của BC.
+ Chứng minh \(ME = MB = MC = MF\). Suy ra đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).
+ Chứng minh tương tự ta có \(CAFD\)và \(ABDE\) cũng là các tứ giác nội tiếp.
Lời giải:
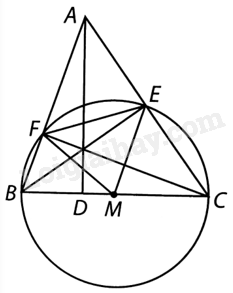
Lấy \(M\) là trung điểm của BC.
Do \(BCE,BCF\) là các tam giác vuông có chung cạnh huyền \(BC\) nên \(ME = MB = MC = MF\).
Do đó đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).
Tương tự, \(CAFD\) và \(ABDE\) cũng là các tứ giác nội tiếp.