Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Giải và trình bày phương pháp giải Giải bài 1 trang 73 vở thực hành Toán 9 – Bài 11. Tỉ số lượng giác của góc nhọn. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang,…
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết:
a) \(AB = 8cm,BC = 17cm\);
b) \(AC = 0,9cm,AB = 1,2cm\).
Hướng dẫn:
– Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
– Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải:
a) (H.4.5a)
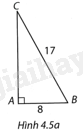
Theo định lí Pythagore, ta có \(A{C^2} + A{B^2} = B{C^2}\)
\(A{C^2} = B{C^2} – A{B^2}\)
\(AC = \sqrt {B{C^2} – A{B^2}} = \sqrt {{{17}^2} – {8^2}} = 15\left( {cm} \right)\)
Từ đó
\(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}};\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{8}{{17}};\\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{15}}{8};\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\)
b) (H.4.5b)
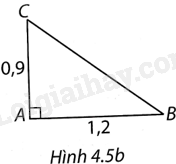
Theo Pythagore, ta có \(BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{{1,2}^2} + {{0,9}^2}} = 1,5\)
Từ đó
\(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5},\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}, \\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4},\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\)