Đáp án Câu hỏi Thực hành 2 trang 114 SGK Toán 9 Kết nối tri thức – Giải phương trình – hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra. Hướng dẫn: Cách 1: Sử dụng câu lệnh Solve ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<.
Câu hỏi/Đề bài:
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}3x – 2y = 4\\2x + y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x + 2y = 0\\2x – 3y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}x\sqrt 5 – \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 – \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\).
Hướng dẫn:
Cách 1: Sử dụng câu lệnh Solve ({ , (}, { , (}) hoặc Solutions ({ , (}, { , (}) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.
Cách 2: Sử dụng câu lệnh Intersect ({ , (}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải:
a)
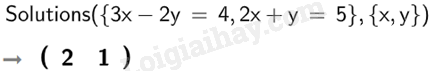
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x – 2y = 4\\2x + y = 5\end{array} \right.\) có nghiệm \(x = 2;y = 1\).
b)
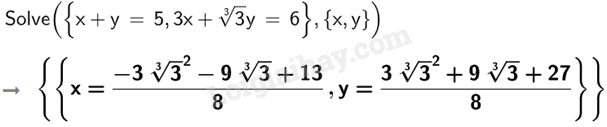
Vậy hệ phương trình \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\) có nghiệm \(x = \frac{{ – 3{{\sqrt[3]{3}}^2} – 9\sqrt[3]{3} + 13}}{8};y = \frac{{3{{\sqrt[3]{3}}^2} + 9\sqrt[3]{3} + 27}}{8}\).
c)
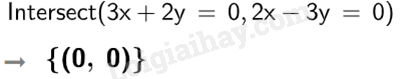
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 0\\2x – 3y = 0\end{array} \right.\) có nghiệm \(x = 0;y = 0\).
d)
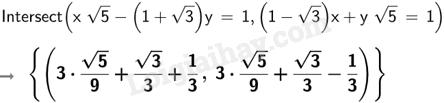
Vậy hệ phương trình \(\left\{ \begin{array}{l}x\sqrt 5 – \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 – \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\) có nghiệm \(x = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} + \frac{1}{3};y = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} – \frac{1}{3}\).