Hướng dẫn giải Câu hỏi Hoạt động 4 trang 6 SGK Toán 9 Kết nối tri thức – Bài 18. Hàm số y = ax² (a ≠ 0). Hướng dẫn: Dựa vào đọc đồ thị hàm số để đưa ra nhận xét.
Câu hỏi/Đề bài:
Xét đồ thị của hàm số \(y = 2{x^2}\) đã vẽ ở HĐ3 (H.6.3).
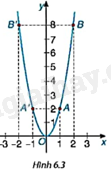
a) Đồ thị nằm về phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị hàm số.
b) So sánh hoành độ và tung độ các cặp điểm thuộc đồ thị: A(1; 2) và \(A’\left( { – 1;2} \right)\); B(2; 8) và \(B’\left( { – 2;8} \right)\).
Từ đó, hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c) Tìm điểm C có hoành độ \(x = \frac{1}{2}\) thuộc đồ thị. Xác định tọa độ của điểm C’ đối xứng với điểm C qua trục tung Oy và cho biết điểm C’ có thuộc đồ thị hàm số hay không.
Hướng dẫn:
a, b) Dựa vào đọc đồ thị hàm số để đưa ra nhận xét.
c) + Thay \(x = \frac{1}{2}\) vào hàm số \(y = 2{x^2}\) để tìm y.
+ Sử dụng tính chất: Hai điểm (x; y) và \(\left( { – x;y} \right)\) đối xứng nhau qua trục tung Oy.
Từ đó tìm được tọa độ C’.
+ Thay tọa độ của điểm C’ vào hàm số \(y = 2{x^2}\) để chứng minh điểm C’ thuộc đồ thị hàm số.
Lời giải:
a) Đồ thị hàm số nằm phía trên trục hoành. Điểm O (0; 0) là điểm thấp nhất của đồ thị.
b) Hai điểm A(1; 2) và \(A’\left( { – 1;2} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
Hai điểm B(2; 8) và \(B’\left( { – 2;8} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
c) Với \(x = \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) thì \(y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}\). Do đó, \(C\left( {\frac{1}{2};\frac{1}{2}} \right)\).
Vì điểm C’ đối xứng với điểm C qua trục Oy nên \(C’\left( { – \frac{1}{2};\frac{1}{2}} \right)\)
Với \(x = – \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) ta có: \(2.{\left( { – \frac{1}{2}} \right)^2} = \frac{1}{2} = {y_{C’}}\)
Do đó, điểm \(C’\left( { – \frac{1}{2};\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\).