Câu hỏi Hoạt động 3 trang 69 Toán 9 Kết nối tri thức: Xét tam giác đều ABC có cạnh bằng 2a. a) Tính đường cao AH của tam giác ABC (H. 4. 7b). b) Tính sin 30^0;cos 30^0;sin 60^0;cos 60^0.

Câu hỏi/Đề bài:

Xét tam giác đều ABC có cạnh bằng 2a.

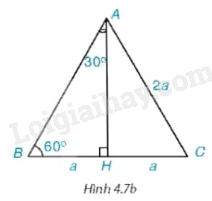
a) Tính đường cao AH của tam giác ABC (H.4.7b) .

b) Tính \(\sin {30^0};\cos {30^0};\sin {60^0};\cos {60^0}.\)

c) Tính \(\tan {30^0};\cot {30^0};\tan {60^0};\cot {60^0}.\)

Hướng dẫn:

Chú ý trong tam giác đều, đường cao vừa là đường phân giác vừa là đường trung tuyến. Từ đó ta tính được cạnh AH và các tỉ số lượng giác liên quan.

Lời giải:

a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó ta có H là trung điểm của BC nên \(BH = HC = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)

Xét tam giác ABH vuông tại H, ta có: \(A{B^2} = A{H^2} + H{B^2}\) (Đjnh lý Pythagore)

Suy ra \({\left( {2a} \right)^2} = A{H^2} + {a^2}\) nên \(A{H^2} = 3a\) hay \(AH = a\sqrt 3 \)

b) Tam giác ABC đều nên \(\widehat A = \widehat B = \widehat C = {60^0}\)

Nên \(\cos {60^0} = \cos \widehat B = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\sin {60^0} = \sin \widehat B = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)

Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác của góc A, do đó \(\widehat {BAH} = \widehat {CAH} = \frac{{\widehat {BAC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)

\(\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)

c) \(\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)

\(\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)

\(\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)

\(\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)