Chu vi phần đất giới hạn bởi tam giác trên là tổng của ba cạnh tam giác. Phân tích, đưa ra lời giải Giải bài tập 9.17 trang 79 SGK Toán 9 tập 2 – Kết nối tri thức – Luyện tập chung trang 78. Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng…
Đề bài/câu hỏi:
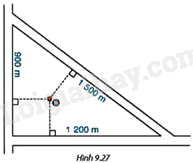
Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m (H.9.27).
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Hướng dẫn:
a) + Chu vi phần đất giới hạn bởi tam giác trên là tổng của ba cạnh tam giác.
+ Chứng minh phần đất giới hạn bởi tam giác là tam giác vuông.
+ Khi đó, diện tích phần đất giới hạn bởi tam giác đó bằng nửa tích hai cạnh góc vuông.
b) Gọi tam giác giới hạn phần đất là ABC, trong đó \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
+ Khách sạn nằm ở vị trí tâm đường tròn nội tiếp tam giác ABC.
+ Từ I kẻ ID vuông góc với AC tại D, IE vuông góc với AB tại E, IF vuông góc với BC.
+ Chứng minh tứ giác AEID là hình vuông, suy ra: \(ID = AD\)
+ Sử dụng tỉ số lượng giác góc nhọn để tính góc BCA, từ đó tính góc ICD.
+ Tính DC theo ID.
+ Sử dụng tỉ số lượng giác góc nhọn trong tam giác IDC để tính ID.
Lời giải:
a) Vì \({900^2} + 1\;{200^2} = 1\;{500^2}\) nên tam giác này là tam giác vuông.
Diện tích phần đất giới hạn bởi tam giác trên là:
\(S = \frac{1}{2}.900.1\;200 = 540\;000\left( {{m^2}} \right)\)
Chu vi phần đất giới hạn bởi tam giác trên là:
\(900 + 1\;200 + 1\;500 = 3\;600\left( m \right)\)
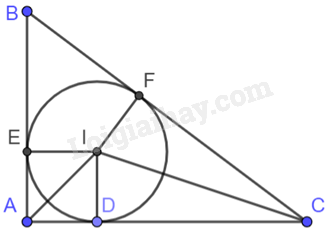
b) Để khách sạn cách đều cả ba con đường thì khách sạn đó trùng với tâm đường tròn nội tiếp tam giác giới hạn phần đất.
Gọi tam giác giới hạn phần đất là ABC, trong đó, \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
Do đó, tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giác ABC.
Tam giác ABC vuông tại A nên
\(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{3}{4} \Rightarrow \widehat {BCA} \approx 36,{87^o}\)
Vì CI là tia phân giác của góc ACB nên
\(\widehat {ICA} = \frac{1}{2}\widehat {ACB} \approx \frac{1}{2}.36,{87^o} \approx 18,{435^o}\)
Từ I kẻ ID vuông góc với AC tại D, IE vuông góc với AB tại E, IF vuông góc với BC tại F.
Khi đó, \(ID = IE = IF\).
Vì ID vuông góc với AC tại D, IE vuông góc với AB tại E nên \(\widehat {IEA} = \widehat {IDA} = {90^o}\).
Tứ giác ADIE có: \(\widehat {EAD} = \widehat {IEA} = \widehat {IDA} = {90^o}\) nên tứ giác ADIE là hình chữ nhật. Mà \(ID = IE\) nên tứ giác ADIE là hình vuông. Do đó, \(ID = AD\)
Ta có: \(DC = AC – AD = 1200 – AD = 1200 – ID\)
Tam giác IDC vuông tại D nên \(\frac{{ID}}{{DC}} = \tan \widehat {ICD}\)
\(\frac{{ID}}{{1200 – ID}} \approx \tan 18,{435^o}\)
\(\begin{array}{l}\frac{{ID}}{{1200 – ID}} \approx 0,33\\ID \approx 0,33\left( {1200 – ID} \right)\end{array}\)
\(ID \approx 297,74\left( m \right)\)
Do đó, khách sạn cách mỗi con đường khoảng 297,74m.