Gọi khung gỗ hình tam giác đều là tam giác ABC. Đồng hồ là đường tròn tâm I. Gợi ý giải Giải bài tập 9.12 trang 76 SGK Toán 9 tập 2 – Kết nối tri thức – Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác. Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn…
Đề bài/câu hỏi:
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

Hướng dẫn:
+ Gọi khung gỗ hình tam giác đều là tam giác ABC. Đồng hồ là đường tròn tâm I, có đường kính 30cm
+ Gọi H là giao điểm của AI và BC nên IH là bán kính đường tròn nội tiếp tam giác ABC.
+ Ta có: \(IH = \frac{{\sqrt 3 }}{6}BC\), từ đó tính được BC.
Lời giải:
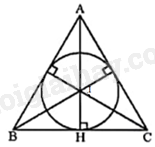
Gọi khung gỗ hình tam giác đều là tam giác ABC.
Đồng hồ là đường tròn tâm I, bán kính \(IH = \frac{{30}}{2} = 15cm\)
Vì (I; IH) nội tiếp tam giác đều ABC nên \(IH = \frac{{\sqrt 3 }}{6}BC\), \(15 = \frac{{\sqrt 3 }}{6}BC\) nên \(BC = 30\sqrt 3 \left( {cm} \right)\)
Vậy độ dài cạnh khung gỗ phía bên trong bằng \(30\sqrt 3 cm\).