Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\). Hướng dẫn cách giải/trả lời Giải bài tập 9.11 trang 76 SGK Toán 9 tập 2 – Kết nối tri thức – Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác. Cho tam giác đều ABC ngoại tiếp đường tròn (I)….
Đề bài/câu hỏi:
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.
Hướng dẫn:
Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).
Lời giải:
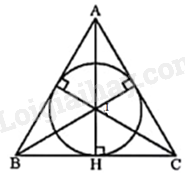
Vì tam giác ABC ngoại tiếp đường tròn (I) và bán kính đường tròn (I) nội tiếp tam giác đều ABC bằng 1cm nên ta có: \(1 = \frac{{\sqrt 3 }}{6}BC \Rightarrow BC = 2\sqrt 3 \left( {cm} \right)\).
Vậy độ dài cạnh tam giác đều bằng \(2\sqrt 3 cm\).