Bài tập 10.5 trang 100 Toán 9 tập 2 – Kết nối tri thức: Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16

Đề bài/câu hỏi:

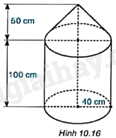
Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16.

a) Tính thể tích của dụng cụ này.

b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).

Hướng dẫn:

a) Thể tích của hình trụ có bán kính đáy R và chiều cao h là: V = S_đáy.h\( = \pi {R^2}h\).

Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).

b) Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).

Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).

Lời giải:

Dụng cụ trên gồm:

+ Hình nón có chiều cao là 50cm, bán kính đáy bằng 40cm.

+ Hình trụ có chiều cao là 100cm, bán kính đáy bằng 40cm.

a) Thể tích của hình nón là: \({V_1} = \frac{1}{3}\pi {.40^2}.50 = \frac{{80\;000\pi }}{3}\left( {c{m^3}} \right)\)

Thể tích của hình trụ là: \({V_2} = \pi {.40^2}.100 = 160\;000\pi \left( {c{m^3}} \right)\)

Thể tích của dụng cụ là: \(V = {V_1} + {V_2} = \frac{{80\;000\pi }}{3} + 160\;000\pi = \frac{{560\;000\pi }}{3}\left( {c{m^3}} \right)\)

b) Đường sinh của hình nón là: \(\sqrt {{{50}^2} + {{40}^2}} = 10\sqrt {41} \left( {cm} \right)\).

Diện tích xung quanh của của hình nón là: \({S_1} = \pi .10\sqrt {41} .40 = 400\sqrt {41} \pi \left( {c{m^2}} \right)\).

Diện tích xung quanh của của hình trụ là: \({S_2} = 2\pi .40.100 = 8000\pi \left( {c{m^2}} \right)\).

Diện tích mặt ngoài của dụng cụ là: \(S = {S_1} + {S_2} = 400\sqrt {41} \pi + 8000\pi = 400\pi \left( {\sqrt {41} + 20} \right)\left( {c{m^2}} \right)\).