Để kiểm tra cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn, ta thay \(x – = {x_0};y = {y_0}\. Phân tích, đưa ra lời giải Giải bài tập 1.5 trang 10 SGK Toán 9 tập 1 – Kết nối tri thức – Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn. Cho các cặp số (left( { – 2;1} right),left( {0;2} right),left( {1;0} right),left( {1,5;3} right),left( {4;…
Đề bài/câu hỏi:
Cho các cặp số \(\left( { – 2;1} \right),\left( {0;2} \right),\left( {1;0} \right),\left( {1,5;3} \right),\left( {4; – 3} \right)\) và hai phương trình
\(\begin{array}{l}5x + 4y = 8,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\3x + 5y = – 3.\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?
c) Vẽ hai đường thẳng \(5x + 4y = 8\) và \(3x + 5y = – 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Hướng dẫn:
Để kiểm tra cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn, ta thay \(x – = {x_0};y = {y_0}\) vào phương trình cần kiểm tra, nếu kết quả luôn đúng ta được cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn.
Lời giải:
a) Thay \(\left( { – 2;1} \right)\) vào phương trình (1) ta có: \(5.\left( { – 2} \right) + 4.1 = -6 \ne 8\)
Thay \(\left( {0;2} \right)\) vào phương trình (1) ta có: \(5.0 + 4.2 = 8\)
Thay \(\left( {1;0} \right)\) vào phương trình (1) ta có: \(5.1 + 4.0 = 5 \ne 8\)
Thay \(\left( {1,5;3} \right)\) vào phương trình (1) ta có: \(5.1,5 + 4.3 = 19,5 \ne 8\)
Thay \(\left( {4; – 3} \right)\) vào phương trình (1) ta có: \(5.4 + 4.\left( { – 3} \right) = 8\) (luôn đúng)
Vậy nghiệm của phương trình (1) là \(\left( {0;2} \right)\) và \(\left( {4; – 3} \right).\)
b) Vì \(\left( { – 2;1} \right)\), \(\left( {1;0} \right)\) và \(\left( {1,5;3} \right)\) không là nghiệm của phương trình (1) nên cũng không là nghiệm của hệ phương trình gồm (1) và (2).
Thay \(\left( {0;2} \right)\) vào phương trình (2) ta có: \(3.0 + 5.2 = 10 \ne – 3\).
Thay \(\left( {4; – 3} \right)\) vào phương trình (2) ta có: \(3.4 + 5.\left( { – 3} \right) = – 3\) (luôn đúng).
Vậy \(\left( {4; – 3} \right)\) là nghiệm của hệ phương trình gồm (1) và (2).
c) Đường thẳng \(5x + 4y = 8\)
Cho \(x = 0 \Rightarrow y = 2 \Rightarrow A\left( {0;2} \right)\)
\(y = 0 \Rightarrow x = \frac{8}{5} \Rightarrow B\left( {\frac{8}{5};0} \right)\)
Đường thẳng \(5x + 4y = 8\) đi qua điểm A và B
Đường thẳng \(3x + 5y = – 3\)
Cho \(x = 0 \Rightarrow y = \frac{{ – 3}}{5} \Rightarrow C\left( {0;\frac{{ – 3}}{5}} \right)\)
\(y = 0 \Rightarrow x = – 1 \Rightarrow D\left( { – 1;0} \right)\)
Đường thẳng \(3x + 5y = – 3\) đi qua điểm C và D
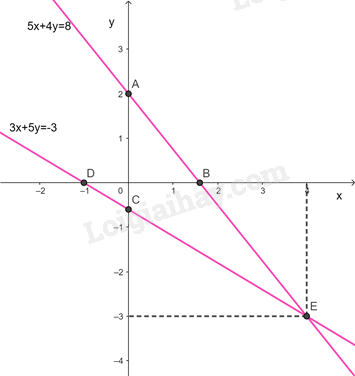
Ta có điểm \(E\left( {4; – 3} \right)\) là giao điểm của đường thẳng \(5x + 4y = 8\) và đường thẳng \(3x + 5y = – 3\) nên \(\left( {4; – 3} \right)\) là nghiệm của hệ phương trình gồm (1) và (2)