Từ diện tích S = a2 (a: độ dài cạnh) từng hình vuông ta tìm được lần lượt cạnh của từng hình vuông – Sau. Trả lời Giải bài tập 8 trang 56 SGK Toán 9 tập 1 – Chân trời sáng tạo – Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai. Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5….
Đề bài/câu hỏi:
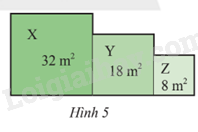
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
Hướng dẫn:
– Từ diện tích S = a2 (a: độ dài cạnh) từng hình vuông ta tìm được lần lượt cạnh của từng hình vuông
– Sau đó tính chu vi của từng hình vuông rồi cộng cá kết quả với nhau.
Lời giải:
Ta có cạnh hình vuông X là: \(\sqrt {32} = 4\sqrt 2 \)m
Suy ra chu vi hình vuông X là: \(4\sqrt 2 .4 = 16\sqrt 2 \)m
Ta có cạnh hình vuông Y là: \(\sqrt {18} = 3\sqrt 2 \)m
Suy ra chu vi hình vuông Y là: \(3\sqrt 2 .4 = 12\sqrt 2 \)m
Ta có cạnh hình vuông Z là: \(\sqrt 8 = 2\sqrt 2 \)m
Suy ra chu vi hình vuông Z là: \(2\sqrt 2 .4 = 8\sqrt 2 \)m
Vậy chu vi của vườn hoa đó là: \(16\sqrt 2 + 12\sqrt 2 + 8\sqrt 2 = 36\sqrt 2 \)m.