Đọc kĩ dữ liệu để vẽ hình. – Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o. Giải và trình bày phương pháp giải Giải bài tập 5 trang 74 SGK Toán 9 tập 2 – Chân trời sáng tạo – Bài 2. Tứ giác nội tiếp. Từ một điểm M nằm ngoài đường tròn (O),…
Đề bài/câu hỏi:
Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Hướng dẫn:
– Đọc kĩ dữ liệu để vẽ hình.
– Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o.
Lời giải:
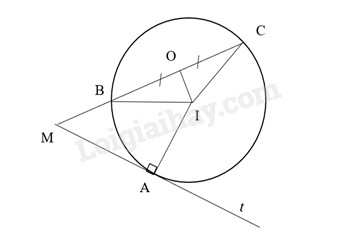
O là trung điểm BC
Và OI cắt BC tại O
Suy ra OI \( \bot \) BC tại O (theo định lí đường kính – dây cung)
Suy ra \(\widehat {IOM} = {90^o}\)
Xét tứ giác AMIO ta có:
\(\widehat {IOM} + \widehat {IAM} = {90^o} + {90^o} = {180^o}\)
Do đó tứ giác AMIO nội tiếp.