Đọc kĩ dữ kiện đề bài để vẽ hình. – Chứng minh \(\Delta \) ADI = \(\Delta \. Hướng dẫn cách giải/trả lời Giải bài tập 3 trang 69 SGK Toán 9 tập 2 – Chân trời sáng tạo – Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E,…
Đề bài/câu hỏi:
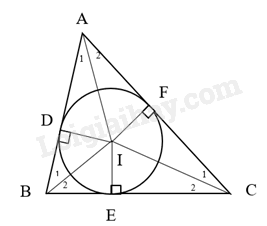
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).
a) Chứng minh 2AD = AB + AC – BC.
b) Tìm các hệ thức tương tự như ở câu a.

Hướng dẫn:
– Đọc kĩ dữ kiện đề bài để vẽ hình.
– Chứng minh \(\Delta \) ADI = \(\Delta \) AFI (c – g – c) nên AD = AF. Tương tự,
\(\Delta \)DBI = \(\Delta \)EIB (c – g – c) nên BD = BE (hai cạnh tương ứng);
\(\Delta \)FCI = \(\Delta \)ECI (c – g – c) nên FC = EC rồi thay vào hệ thức
2AD = AB + AC – BC để chứng minh.
Lời giải:
a) Vì I là tâm đường tròn nội tiếp tam giác ABC
Suy ra I là giao điểm của ba đường phân giác tam giác ABC
\(\widehat {{A_1}} = \widehat {{A_2}};\widehat {{B_1}} = \widehat {{B_2}};\widehat {{C_1}} = \widehat {{C_2}}\).
Xét \(\Delta \)ADI và \(\Delta \)AFI có:
ID = IF = R;
\(\widehat {{A_1}} = \widehat {{A_2}}\) (chứng minh trên);
AI chung.
Suy ra \(\Delta \)ADI = \(\Delta \)AFI (c – g – c).
Do đó, AD = AF (hai cạnh tương ứng) (1).
Chứng minh tương tự, ta được:
\(\Delta \)DBI = \(\Delta \)EIB (c – g – c) suy ra BD = BE (hai cạnh tương ứng) (2).
\(\Delta \)FCI = \(\Delta \)ECI (c – g – c) suy ra FC = EC (hai cạnh tương ứng) (3).
– Ta có: AB + AC – BC = AD + BD + AF + FC – BE – EC (4).
Thay (1), (2), (3) vào (4) ta được:
AB + AC – BC = AD + BE + AD + EC – BE – EC = 2AD (điều phải chứng minh).
b) Các hệ thức tương tự như ở câu a:
2AF = AB + AC – BC;
2BD = 2BE = AB + BC – AC;
2EC = 2FC = AC + BC – AB.