Đáp án Câu hỏi Luyện tập 4 trang 109 SGK Toán 9 Cánh diều – Bài 3. Tiếp tuyến của đường tròn. Gợi ý: Dựa vào tính chất 2 tiếp tuyến cắt nhau và tỉ số lượng giác để làm bài toán.
Câu hỏi/Đề bài:
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng \(c,d\) qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\) biết \(\widehat {AMB} = 120^\circ \). Chứng minh \(AB = R\).
Hướng dẫn:
Dựa vào tính chất 2 tiếp tuyến cắt nhau và tỉ số lượng giác để làm bài toán.
Lời giải:
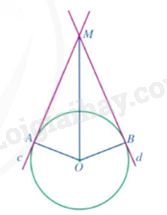
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên \(\widehat {AMO} = \widehat {BMO} = \frac{{\widehat {AMB}}}{2} = 60^\circ \).
Xét tam giác \(AMO\) vuông tại \(A\) có:
\(\widehat {AMO} + \widehat {MOA} = 90 \Rightarrow 60^\circ + \widehat {MOA} = 90^\circ \Rightarrow \widehat {MOA} = 30^\circ \).
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên \(\widehat {AOB} = 2\widehat {AOM} = 2.30^\circ = 60^\circ \).
Xét tam giác \(AOB\) có: \(OA = OB = R\) nên tam giác \(AOB\) cân tại \(O\).
Lại có \(\widehat {AOB} = 60^\circ \) suy ra tam giác \(AOB\) là tam giác đều.
Vậy \(AO = OB = AB = R\).