Hướng dẫn giải Câu hỏi Hoạt động 4 trang 115 – Bài 4. Góc ở tâm. Góc nội tiếp. Gợi ý: Dựa vào các kiến thức đã học về đường tròn để xác định.
Câu hỏi/Đề bài:
SGK Toán 9 Cánh diều
Cho góc \(AIB\) nội tiếp đường tròn tâm \(O\) đường kính \(IK\) sao cho tâm \(O\) nằm trong góc đó (Hình 57).
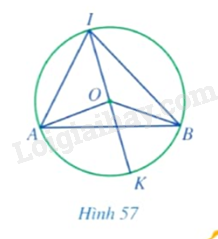
a) Các cặp góc \(\widehat {OAI}\) và \(\widehat {OIA};\widehat {OBI}\) và \(\widehat {OIB}\) có bằng nhau hay không?
b) Tính các tổng \(\widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}\).
c) Tính các tổng \(\widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}\).
d) So sánh \(\widehat {AOK}\) và \(2\widehat {OIA},\widehat {BOK}\) và \(2\widehat {OIB},\widehat {AOB}\) và \(2\widehat {AIB}\).
Hướng dẫn:
Dựa vào các kiến thức đã học về đường tròn để xác định.
Lời giải:
a) Do \(OI = OA = R\) nên tam giác \(IOA\) cân tại \(O\) suy ra \(\widehat {OAI} = \widehat {OIA}\)
Do \(OI = OB = R\) nên tam giác \(IOB\) cân tại \(O\) suy ra \(\widehat {OBI} = \widehat {OIB}\)
b) Xét tam giác \(AOI\) cân tại \(O\) có:
\(\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ \Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ \Rightarrow \widehat {AOI} + 2\widehat {OIA} = 180^\circ \)
Xét tam giác \(BOI\) cân tại \(O\) có:
\(\widehat {BOI} + \widehat {OIB} + \widehat {OBI} = 180^\circ \Rightarrow \widehat {BOI} + \widehat {OIB} + \widehat {OIB} = 180^\circ \Rightarrow \widehat {BOI} + 2\widehat {OIB} = 180^\circ \)
c) Ta có: \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) (hai góc kề bù)
\(\widehat {BOI} + \widehat {BOK} = 180^\circ \) (hai góc kề bù)
d) Do \(\widehat {AOI} + 2\widehat {OIA} = 180^\circ \) lại có \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) nên \(2\widehat {OIA} = \widehat {AOK}\)
Do \(\widehat {BOI} + 2\widehat {OIB} = 180^\circ \) lại có \(\widehat {BOI} + \widehat {BOK} = 180^\circ \) nên \(2\widehat {OIB} = \widehat {BOK}\)
Ta có: \(\widehat {OIA} + \widehat {OIB} = \widehat {AIB} \Rightarrow 2\left( {\widehat {OIA} + \widehat {OIB}} \right) = 2\widehat {AIB} \Rightarrow 2\widehat {OIA} + 2\widehat {OIB} = 2\widehat {AIB}\)
Mà \(2\widehat {OIA} = \widehat {AOK},2\widehat {OIB} = \widehat {BOK}\) nên \(\widehat {AOK} + \widehat {BOK} = 2\widehat {AIB} \Rightarrow \widehat {AOB} = 2\widehat {AIB}\)