Dựa vào các kiến thức đã học để giải bài toán. Hướng dẫn giải Giải bài tập 7 trang 100 SGK Toán 9 tập 1 – Cánh diều – Bài 1. Đường tròn. Vị trí tương đối của hai đường tròn. Cho hai đường tròn cùng tâm \(\left( {O;R} \right),\left( {O;r} \right)\) với \(R > r\). Các điểm \(A,B\…
Đề bài/câu hỏi:
Cho hai đường tròn cùng tâm \(\left( {O;R} \right),\left( {O;r} \right)\) với \(R > r\). Các điểm \(A,B\) thuộc đường tròn \(\left( {O;R} \right)\), các điểm \(A’,B’\) thuộc đường tròn \(\left( {O;r} \right)\) sao cho \(O,A,A’\) thẳng hàng; \(O,B,B’\) thẳng hàng và điểm \(O\) không thuộc đường thẳng \(AB\). Chứng minh:
a) \(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}}\).
b) \(AB//A’B’\).
Hướng dẫn:
Dựa vào các kiến thức đã học để giải bài toán.
Lời giải:
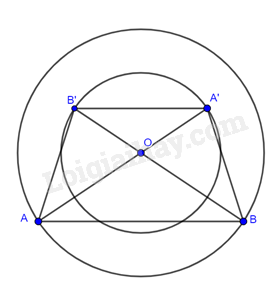
a) Do các điểm \(A,B\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OA = OB = R\).
Do các điểm \(A’,B’\) thuộc đường tròn \(\left( {O;r} \right)\) nên \(OA’ = OB’ = r\).
Ta có: \(\frac{{OA’}}{{OA}} = \frac{R}{r};\frac{{OB’}}{{OB}} = \frac{R}{r}\).
Vậy \(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}}\).
b) Xét tam giác \(OAB\) có: \(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}}\)
Nên \(AB//A’B’\) (Định lí Thalet đảo).