Chứng minh \(\widehat C = \widehat D\) (do cùng bù với góc A). Phân tích, đưa ra lời giải Giải bài tập 5 trang 78 SGK Toán 9 tập 2 – Cánh diều – Bài 2. Tứ giác nội tiếp đường tròn. Cho hình thang ABCD (AB//CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân….
Đề bài/câu hỏi:
Cho hình thang ABCD (AB//CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.
Hướng dẫn:
Chứng minh \(\widehat C = \widehat D\) (do cùng bù với góc A).
Lời giải:
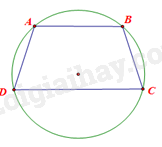
Ta có: ABCD nội tiếp đường tròn nên \(\widehat A + \widehat C = 180^\circ .\) Hơn nữa \(\widehat A + \widehat D = 180^\circ \) (do AB//CD)
Suy ra \(\widehat C = \widehat D\).
Xét hình thang ABCD có AB//CD, \(\widehat C = \widehat D\) nên ABCD là hình thang cân (dhnb).