Dựa vào tính chất đối xứng của đường tròn để chứng minh. Gợi ý giải Giải bài tập 3 trang 100 SGK Toán 9 tập 1 – Cánh diều – Bài 1. Đường tròn. Vị trí tương đối của hai đường tròn. Cho đoạn thẳng \(MN\) và đường thẳng \(a\) là đường trung trực của đoạn thẳng \(MN\). Điểm \(O\…
Đề bài/câu hỏi:
Cho đoạn thẳng \(MN\) và đường thẳng \(a\) là đường trung trực của đoạn thẳng \(MN\). Điểm \(O\) thuộc đường thẳng \(a\).
a) Vẽ đường tròn tâm \(O\) bán kính \(R = OM\).
b) Chứng minh điểm \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Hướng dẫn:
Dựa vào tính chất đối xứng của đường tròn để chứng minh.
Lời giải:
a)
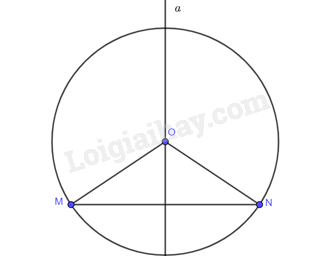
b) Do \(O\) thuộc đường trung trực của \(MN\) nên \(OM = ON\).
Lại có \(OM = R\) suy ra \(ON = R\).
Vậy điểm \(N\) thuộc đường tròn \(\left( {O;R} \right)\).