Áp dụng \(\tan \widehat {BCA} = \frac{{BA}}{{AC}}\), từ đó tính được AC. Trả lời Giải bài 9 trang 82 sách bài tập toán 9 – Cánh diều tập 1 – Bài 1. Tỉ số lượng giác của góc nhọn. Từ vị trí B của toà nhà cao 70 m, một tia sáng chiếu xuống một ô tô đang đỗ…
Đề bài/câu hỏi:
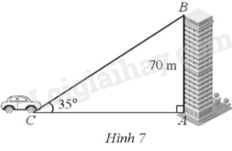
Từ vị trí B của toà nhà cao 70 m, một tia sáng chiếu xuống một ô tô đang đỗ tại vị trí C. Góc tạo bởi tia sáng và phương nằm ngang là \(\widehat {ACB} = 35^\circ \) (Hình 7). Hỏi ô tô đỗ cách chân toà nhà (ở vị trí A) bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Hướng dẫn:
Áp dụng \(\tan \widehat {BCA} = \frac{{BA}}{{AC}}\), từ đó tính được AC.
Lời giải:
Xét tam giác ABC vuông tại A, ta có \(\tan \widehat {BCA} = \frac{{BA}}{{AC}}\) hay \(\tan 35^\circ = \frac{{70}}{{AC}}\),
suy ra \(AC = \frac{{70}}{{\tan 35^\circ }} \approx 99,97\)m.
vậy ô tô đỗ cách chân toà nhà khoảng 99,97m.