Chứng minh hai góc kề ở đáy của tam giác bằng nhau. Chứng minh \(\widehat {EAN} = \widehat {NAM}\). Chứng minh ∆MAB ᔕ ∆BAC (g. Vận dụng kiến thức giải Giải bài 7 trang 107 sách bài tập toán 9 – Cánh diều tập 2 – Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn. Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N….
Đề bài/câu hỏi:
Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:
a) Các tam giác AEN và CMB là các tam giác cân;
b) AN là phân giác của góc EAM;
c) AB.BC = BM.AC.
Hướng dẫn:
Chứng minh hai góc kề ở đáy của tam giác bằng nhau.
Chứng minh \(\widehat {EAN} = \widehat {NAM}\).
Chứng minh ∆MAB ᔕ ∆BAC (g.g) suy ra tỉ số đồng dạng.
Lời giải:
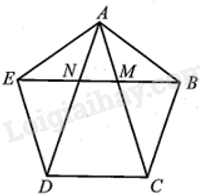
a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và
\(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}\).
Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.
Do đó, \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{{{540}^o}}}{5} = {108^o}\).
Xét ∆AEB cân tại A (do AB = AE) ta có:
\(\widehat {ABE} = \widehat {AEB} = \frac{{{{180}^o} – \widehat {EAB}}}{2} = \frac{{{{180}^o} – {{108}^o}}}{2} = {36^o}\) hay \(\widehat {ABM} = \widehat {AEN} = {36^o}\).
Tương tự, đối với ∆EAD cân tại E ta có: \(\widehat {EAD} = \widehat {EDA} = {36^o}\) hay \(\widehat {EAN} = {36^o}\).
Do đó ta có \(\widehat {EAN} = \widehat {NEA} = {36^o}\) .Suy ra ∆AEN cân tại N.
Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = {36^o}\))
Suy ra \(\widehat {AMB} = {180^o} – 2\widehat {MAB} = {180^o} – {2.36^o} = {108^o}\).
Mặt khác: \(\widehat {CMB} = {180^o} – \widehat {AMB} = {180^o} – {108^o} = {72^o}\)
\(\widehat {MBC} = \widehat {ABC} – \widehat {ABM} = {180^o} – {36^o} = {72^o}\)
Suy ra tam giác CMB cân tại C.
b) Ta có \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)
Suy ra \(\widehat {NAM} = \widehat {EAB} – \widehat {EAN} – \widehat {MAB} = {180^o} – {36^o} – {36^o} = {36^o}\).
Do đó \(\widehat {EAN} = \widehat {NAM} = {36^o}\).
Vì vậy AN là phân giác của góc EAM.
c) Xét ∆MAB và ∆BAC có:
\(\widehat {AMB} = \widehat {ABC} = {108^o}\) và \(\widehat {BAC}\) là góc chung.
Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.