Bài 60 trang 125 SBT toán 9 – Cánh diều tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng 5π R/6\

Đề bài/câu hỏi:

Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng \(\frac{{5\pi R}}{6}\)

a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH.

b) Tính độ dài các cung AC, BC theo R.

c) Kẻ OK vuông góc với AB tại K, tia OK cắt đường tròn (O) tại E. Tính diện tích hình quạt tròn EOB (giới hạn bởi cung nhỏ BE và hai bán kính OE, OB) theo R.

d) Tính tỉ số phần trăm giữa diện tích hình quạt tròn BOC (giới hạn bởi cung nhỏ

BC và hai bán kính OB, OC) và diện tích hình quạt tròn AOC (giới hạn bởi cung nhỏ AC và hai bán kính OA, OC).

Hướng dẫn:

a) Chứng minh tam giác AHC vuông cân, từ đó tính số đo cung CB.

b) Bước 1: Tính số đo cung nhỏ AB, AC.

Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\).

c) Bước 1: Tính \(\widehat {BOE}\), từ đó suy ra số đo cung nhỏ EB.

Bước 2: Áp dụng công thức \(S = \frac{{\pi {R^2}n}}{{360}}\).

d) Tỉ số phần trăm = (diện tích quạt tròn BOC : Diện tích quạt tròn AOC).100%.

Lời giải:

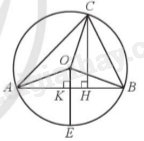
a) Ta có \(CH \bot AB\) nên \(\widehat {CHA} = 90^\circ \).

Xét tam giác AHC có \(\widehat {CHA} = 90^\circ \), \(HA = CH\) nên tam giác AHC vuông cân tại H, do đó \(\widehat {CAH} = 45^\circ \).

Mặt khác, góc CAH là góc nội tiếp chắn cung CB của (O) nên sđ\(\overset\frown{CB}=2\widehat{CAH}=2.45{}^\circ =90{}^\circ \).

Vậy điểm C nằm trên cung lớn AB sao cho số đo cung CB bằng 90⁰.

b) Độ dài cung nhỏ CB có số đo 90⁰ của (O; R) là \(\frac{{\pi R.90}}{{180}} = \frac{{\pi R}}{2}\).

Độ dài cung nhỏ AB có số đo n⁰ bằng \(\frac{{5\pi R}}{6}\) nên \(\frac{{\pi R.n}}{{180}} = \frac{{5\pi R}}{6}\), hay \(n = 150^\circ \), do đó số đo góc ở tâm \(\widehat {AOB} = 150^\circ \), suy ra sđ\(\overset\frown{AB}=150{}^\circ \).

Số đo cung nhỏ AC bằng \(360{}^\circ -\text{sđ}\overset\frown{CB}-\text{sđ}\overset\frown{AB}=360{}^\circ -90{}^\circ -150{}^\circ =120{}^\circ \).

Độ dài cung nhỏ AC là \(\frac{{\pi R.120}}{{180}} = \frac{{2\pi R}}{3}\).

c) Ta có \(OA = OB\left( { = R} \right)\) nên tam giác OAB cân tại O, mà \(OK \bot AB\) do đó OK là đường cao đồng thời là đường phân giác của tam giác OAB, suy ra \(\widehat {AOK} = \widehat {BOK} = \frac{{\widehat {AOB}}}{2} = \frac{{150^\circ }}{2} = 75^\circ \).

Góc BOK hay góc BOE là góc ở tâm chắn cung EB của (O) nên sđ \(\overset\frown{EB}=\widehat{BOE}=75{}^\circ \).

Diện tích quạt tròn EOB là \(\frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {R^2}.75}}{{360}} = \frac{{5\pi {R^2}}}{{24}}\).

a) Vì số đo cung CB bằng 90⁰ nên góc COB là góc ở tâm chắn cung CB cũng bằng 90⁰.

Diện tích quạt tròn BOC là \(\frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {R^2}.90}}{{360}} = \frac{{\pi {R^2}}}{4}\)

Diện tích quạt tròn AOC là \(\frac{{\pi {R^2}.120}}{{360}} = \frac{{\pi {R^2}}}{3}\)

Tỉ số phần trăm giữa diện tích quạt tròn BOC và Diện tích quạt tròn AOC là

\(\frac{{\pi {R^2}}}{4}:\frac{{\pi {R^2}}}{3}.100\% = 75\% \)