Diện tích cần tìm = diện tích \(\Delta OAB\) + diện tích quạt tròn OAD + diện tích quạt tròn OBC. Bước 1. Gợi ý giải Giải bài 46 trang 122 sách bài tập toán 9 – Cánh diều tập 1 – Bài 5. Độ dài cung tròn – diện tích hình quạt tròn – diện tích hình vành khuyên. Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM,…
Đề bài/câu hỏi:
Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’, vuông góc với OM và đường kính CD song song với AB (Hình 50). Tính (làm tròn kết quả đến hàng đơn vị của centimét vuông):
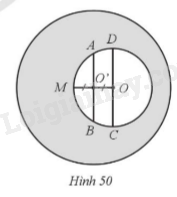
a) Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O);
b) Diện tích của phần tô màu xám.
Hướng dẫn:
a) Diện tích cần tìm = diện tích \(\Delta OAB\) + diện tích quạt tròn OAD + diện tích quạt tròn OBC.
Bước 1: Chứng minh OAMB là hình thoi, từ đó chứng minh tam giác OAM đều và \(\widehat {AOM} = 60^\circ \).
Bước 2: Chứng minh tam giác OAB cân, từ đó tính được \(\widehat {OAB} = \widehat {BAO} = 30^\circ \) và AB.
Bước 3: Tính diện tích tam giác OAB.
Bước 4: Chứng minh \(AB//CD\), từ đó tính được góc ở tâm chắn cung AD và BC.
Bước 5: Tính diện tích quạt tròn OAD và OBC của (O).
b) Diện tích của phần tô màu xám = diện tích (O’) – diện tích (O).
Lời giải:
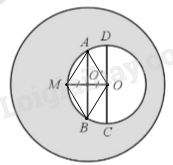
a) Ta có \(OA = OB\) (cùng bằng bán kính (O)) nên tam giác OAB là tam giác cân tại O.
Mà OO’ là đường cao (do \(OM \bot AB\)) của tam giác OAB nên đồng thời là đường trung tuyến, do đó \(O’A = O’B = \frac{{AB}}{2}\).
Xét tứ giác OAMB có \(OM \bot AB\), \(O’A = O’B\), \(O’M = O’O\) nên OAMB là hình thoi.
Xét tam giác OAM có \(OA = OM\) (cùng bằng bán kính (O)), \(OA = MA\) (OAMB là hình thoi) nên tam giác OAM đều, do đó \(\widehat {AOM} = 60^\circ \).
Xét \(\Delta AOO’\) vuông tại O’ có: \(\widehat {O’AO} + \widehat {O’OA} = 90^\circ \) hay \(\widehat {O’AO} = 90^\circ – \widehat {O’OA} = 90^\circ – 60^\circ = 30^\circ \)
Suy ra \(\widehat {OAB} = \widehat {BAO} = 30^\circ \) (do tam giác OAB cân tại O).
Có O’ là trung điểm của MO nên \(O’M = O’O = \frac{{MO}}{2} = \frac{8}{2} = 4\) (cm).
Xét tam giác AOO’ vuông tại O’, ta có:
\(AO’ = OO’.\tan \widehat {AOO’} = 4.\tan 60^\circ = 4\sqrt 3 \) (cm).
Do \(O’A = \frac{{AB}}{2}\) nên \(AB = 2O’A = 2.4\sqrt 3 = 8\sqrt 3 \) (cm).
Diện tích tam giác OAB là:
\(\frac{1}{2}.OO’.AB = \frac{1}{2}.4.8\sqrt 3 = 16\sqrt 3 \) (cm2).
Do \(MO \bot AB,AB//CD\) nên \(MO \bot CD\) hay \(\widehat {MOD} = \widehat {MOC} = 90^\circ \)
Có \(AB//CD\) nên \(\widehat {BAO} = \widehat {AOD} = 30^\circ \) và \(\widehat {ABO} = \widehat {BOC} = 30^\circ \) (các cặp góc so le trong), do đó số đo cung tròn AD và BC của (O) là 30⁰.
Vì 2 hình quạt tròn OAD và OBC của (O) có cùng bán kính 8cm, và số đo cung là 30⁰ nên tổng diện tích 2 hình quạt tròn là:
\(2.\frac{{\pi {{.8}^2}.30}}{{360}} = \frac{{32\pi }}{3}\) (cm2).
Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O) là:
\(16\sqrt 3 + \frac{{32\pi }}{3} \approx 61\) (cm2).
b) Diện tích đường tròn (O) là:
\({16^2}\pi = 256\pi \) (cm2).
Diện tích đường tròn (O’) là:
\({8^2}\pi = 64\pi \) (cm2).
Diện tích phần tô màu xám là:
\(256\pi – 64\pi \approx 603\) (cm2).