Bước 1: Chứng minh AOMO’ là hình vuông để suy ra số đo cung AmM và AnM và độ dài bán kính 2 đường tròn. Gợi ý giải Giải bài 40 trang 121 sách bài tập toán 9 – Cánh diều tập 1 – Bài 5. Độ dài cung tròn – diện tích hình quạt tròn – diện tích hình vành khuyên. Cho tam giác ABE vuông cân tại A với AB = AE = 2a….
Đề bài/câu hỏi:
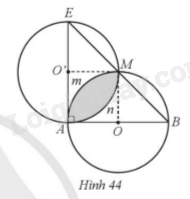
Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44). Tính theo a:
a) Độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’);
b) Diện tích của phần tô màu xám theo a.
Hướng dẫn:
a) Bước 1: Chứng minh AOMO’ là hình vuông để suy ra số đo cung AmM và AnM và độ dài bán kính 2 đường tròn.
Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\)
b) Diện tích tô đậm cần tìm = diện tích tạo bởi cung AnM và dây AM + diện tích tạo bởi cung AmM và dây AM.
Trong đó:
Diện tích tạo bởi cung AnM và dây AM = diện tích quạt của (O’;R), cung AnM – diện tích tam giác O’AM.
Diện tích tạo bởi cung AmM và dây AM = diện tích quạt của (O;R), cung AmM – diện tích tam giác O’AM.
Lời giải:
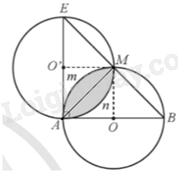
a) Ta có \(O’A = O’E = O’M = \frac{{AE}}{2}\) (cùng bằng bán kính (O’)) và \(OA = OB = OM = \frac{{AB}}{2}\) (cùng bằng bán kính (O))
Mà AB = AE = 2a nên \(O’A = O’E = O’M = OA = OB = OM = a\)
Xét tứ giác AOMO’ có \(O’A = O’M = OA = OM\) và\(\widehat {O’AO} = 90^\circ \) nên AOMO’ là hình vuông. Suy ra \(\widehat {AO’M} = \widehat {AOM} = 90^\circ \).
Mà \(\widehat {AO’M}\) là góc ở tâm chắn cung AnB của (O’) và \(\widehat {AOM}\) là góc ở tâm chắn cung AmB của (O) nên sđ \(\overset\frown{AnB}\)= sđ \(\overset\frown{AmB}\) \( = 90^\circ \). Hơn nữa 2 đường tròn (O) và (O’) có cùng bán kính là a , do đó độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’) là
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .a.90}}{{180}} = \frac{{\pi a}}{2}\)
b) Diện tích quạt tròn của (O’;R), cung AnM có số đo \(90^\circ \) là:
\({S_1} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi .{a^2}.90}}{{360}} = \frac{{\pi .{a^2}}}{4}\)
Diện tích tam giác O’AM là
\({S_2} = \frac{1}{2}O’A.O’M = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\).
Diện tích phần tô đậm được giới hạn bởi cung AnM và dây AM là:
\(S’ = {S_1} – {S_2} = \frac{{\pi {a^2}}}{4} – \frac{{{a^2}}}{2} = \frac{{\left( {\pi – 2} \right){a^2}}}{4}\)
Diện tích quạt tròn của (O;R), cung AmM có số đo \(90^\circ \) là:
\({S_1}’ = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi .{a^2}.90}}{{360}} = \frac{{\pi .{a^2}}}{4}\)
Diện tích tam giác OAM là
\({S_2}’ = \frac{1}{2}OA.OM = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\).
Diện tích phần tô đậm được giới hạn bởi cung AmM và dây AM là:
\(S = {S_1}’ – {S_2}’ = \frac{{\pi {a^2}}}{4} – \frac{{{a^2}}}{2} = \frac{{\left( {\pi – 2} \right){a^2}}}{4}\)
Diện tích phần tô đậm cần tìm là:
\(S’ + S = \frac{{\left( {\pi – 2} \right){a^2}}}{4} + \frac{{\left( {\pi – 2} \right){a^2}}}{4} = \frac{{\left( {\pi – 2} \right){a^2}}}{2}\)